Wie kann ich mit Hilfe von integrieren Volumen berechnen, wenn es sich nicht um einen Rotationskörper handelt?

Question

Hallo alle zusammen :)

 

Ich habe morgen Mathe Prüfung, kann Gott sei Dank schon alles. Jedoch gibt es noch eine Sache, bei welcher ich nicht weiterkomm: Volumsberechnung von Körpern ohne Rotationsform.

Also ohne jegliche Funktionen oder Koordinaten, jedoch ist es nötig das Volumen mit Integralen auszurechnen, da sich die Seitenkanten nicht linear verhalten (außer bei Grundfläche und der Fläche oben, welche eine andere Fläche hat als die Grundfläche).

 

Ich weiß dass man eine Funktion aufstellen muss, und die Intervallgrenzen sind die Höhe, mehr weiß ich jedoch nicht, und meine Kollegen können mir leider auch nicht weiterhelfen :(.

 

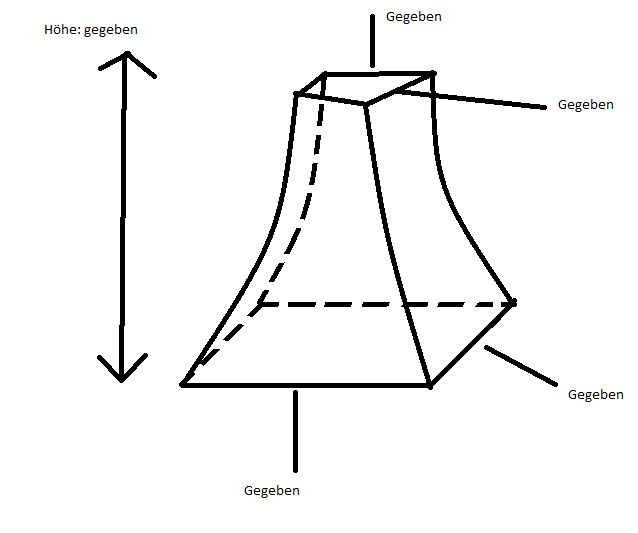
Hier noch ein Bild, um sich das ganze etwas vorstellen zu können. Jedoch ist dieses Bild nicht 1:1 mein Problem, das wäre ja noch relativ einfach. In meinem Problem sind die Kanten alle kurvig, also nicht linear. Ich hoffe, ihr wisst was ich meine.

 

Gegeben habe ich übrigens Höhe, die Länge der Seiten der Grundfläche und die Länge der Seiten auf der Fläche oben, und die jeweils waagrecht parallel stehenden seiten sind gleich lang (bei unseren Aufgaben).

 

Comments

Wenn du die Fläche auf der Höhe z als Funktion f von z ausdrücken kannst,

Kannst du für das Volumen f(z) von 0 bis h integrieren. Also:

₀∫ ^h f(z) dz = Volumen.

Das dz in dieser Formel ist sozusagen die Dicke der Scheibchen, die du hier addierst.

---

Lu, geht das generell so, wie du es sagst bei beliebigen Körpern in R^3 ?

---

Ja. Das gilt in beliebigen Körpern im R^3.

Das ganze wird oft auch als Doppelintegral geschrieben. Z.B. kann man so über das Volumen einer Kugel integrieren. Das geht zwar auch über ein Rotationsintegral aber es geht auch anders.

Answer 1

Das du das auf irgend eine Art und Weise modellierst, bleibt dir beim Volumsintegral nicht erspart. In der Theorie führt man alles auf eine Menge zurück und integriert dann über diese.

Also es gehören alle (x,y,z) zu dieser Menge die durch irgendwelche Funktionen begrenzt werden. Oder irgendwelche anderen Bedingungen. Wie das genau formal aussieht, ist dann schon höhere Mathematik und würde zu weit führen hier alles in eine Antwort zu pressen.

Eine gute Einführung in die Theorie wird in Harro Heusers Lehrbuch der Analysis Teil 2 (Kapitel: Mehrfache Rieman Integrale) geboten.

Die räumliche Figur in einer Menge darzustellen, mag jetzt nicht immer einfach klingen, aber das ist halt die Aufgabe eines Mathematikers dies zu modellieren.


zu dem was in den Kommentaren noch stand:

Eine oft wirkungsvolle Methode ist auch die Zerlegung in Scheiben einer räumlichen Figur. Diese Scheiben sollte man in einer Funktion S(h) darstellen. (h... sei hier die Höhe). Dann kann man über die Höhe integrieren und summiert so die einzelnen Scheiben auf.

Eigentlich ist aber diese Zerlegung auch nichts anderes als die darstellung einer Menge und dann wird über diese integriert. Es gibt halt einen Satz von Fubini der uns sagt, dass wir bei bestimmten Voraussetzungen diese Menge zerlegen können. Um nochmal auf die Methode mit den Scheiben zurückzukommen. So zerlege ich eine 3 dimensionale Menge die das Volumen im Ganzen beschreibt, in eine 2 dimensionale die die Flächen (Scheiben) beschreiben und in eine 1 dimensionale die die Höhe beschreibt.


Hoffe das gibt einen kleinen Überblick.