Skizze vorweg, damit du weisst, was zu berechnen ist.
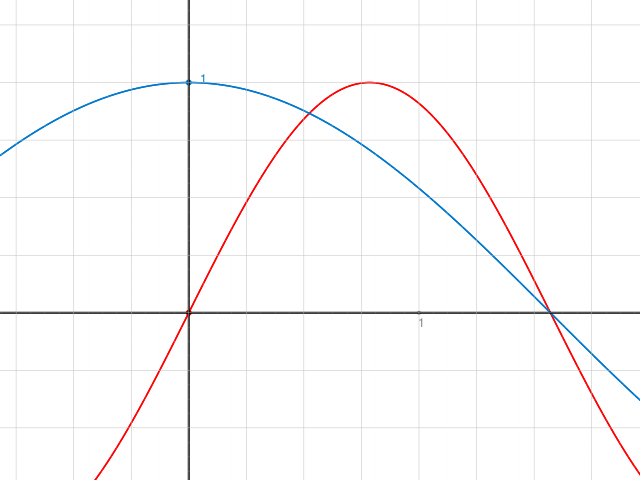
1. Berechne die Schnittstellen durch gleichsetzen der beiden Funktionen.
Wie in der Skizze kommt in der Rechnung (vgl. Kommentar) etwas mehr als 0.5 (exakt π/3) und etwas mehr als 1.5 (exakt π/2) raus. (Der Schnittwinkel bei etwa 0.5 misst in der Skizze geschätzt ca. 70°, der andere ca. 45°)
2. Berechne die Ableitungen beider Funktionen an der Schnittstelle.
(cos x)' = - sin x
m1 = -sin π/2 = -1
m2 = - sin π/6 = -0.5
(sin (2x))' = 2*cos(2x)
m3 = 2*cos (π/2) = 0
m4 = 2 cos (2*π/6) = 2 cos (π/3) = 1
3. Steigungswinkel der beiden Kurven bestimmen: Die beiden Zahlen aus 2. mit arctan in ° umwandeln.
(cos x)' = - sin x
m1 = -sin 0 = -1 ---> 45°
m2 = - sin π/6 = -0.5 ----> -26.565°
(sin (2x))' = 2*cos(2x)
m3 = 2*cos (π/2) = 0 → 0°
m4 = 2 cos (2*π/6) = 2 cos (π/3) = 1 -----> 45°
4. Schittwinkel = Differenz der beiden gefundenen Winkel. Sollte ein stumpfer Winkel rauskommen: 180° - diesen Winkel berechnen.
Schnittwinkel bei x1= 0. m1- m3 = 45° = π/4
Schnittwinkel bei x2= π/6=30°. m4- m2 = 71.565° = 0.39758π
Rechenfehler bitte melden.