Annahme: hier braucht's tatsächlich keine Klammern. D.h. es steht nur die 1 über und die 2 unter dem Bruchstrich?
Wenn ja, kannst du sinx auslammern, da tanx =( sinx)/(cosx)
Somit
sinx (1 - 1/(2cox)) = 0
1. Möglichkeit sinx = 0. → x1 = 0°, x2= 180°, wenn noch im Bereich 360°
2. Möglichkeit:
1=1/(2cosx)
cosx = 1/2 → x3=60°, x4 = 360°-60° = 300°
L ={0°, 60°, 300°, 360°} falls beide Randpunkte im gesuchte Bereich liegen.
Kontrolle: Skizze im Bereich x von 0 bis 2π also etwas mehr als 6 in Bogenmass. 60° ist etwas bei 1 und 300° etwas über 5.
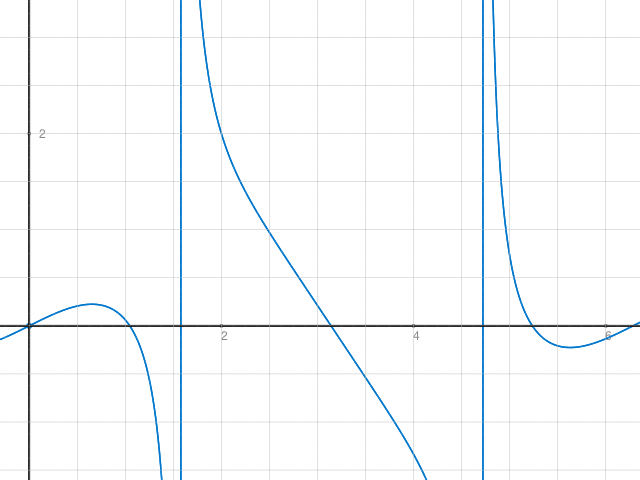
Nebenprodukt: Definitionsbereich: D = [0°,360°] \ {90°, 270°}. D.h. ohne die Winkel, für die tanx nicht definiert ist.
Wertebereich: ganz R. Wegen einfachen Nulldurchgängen und Polen.