a) Sei Φ: I × U → ℝn eine C1-Funktion mit der Eigenschaft, dass für jedes t ∈ I die Funktion Φt: x ↦ Φ(t,x) ein C1-Diffeomorphismus ist. Zeigen Sie, dass φ: I ↦ U genau dann eine Lösung der DGL x' = f(t,x) ist, wenn
ψ = Φt(φ) folgende DGL löst:
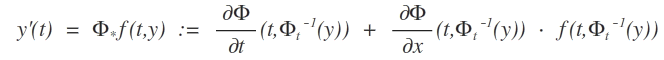
b) Betrachten Sie für a,b,c: I → ℝ die DGL
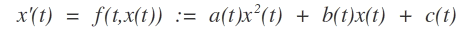
Zeigen Sie: Wenn μ(t) eine spezielle Lösung der obigen DGL ist, ist y'(t) = Φ*f(t,y) mit Φ(t,x) = x - μ(t) eine Bernoullische DGL.