Graphendiskussion mit sin und cos

Question

Wir müssen eine Graphendiskussion machen von der Funktion:


sin( 2x ) +2 cos x,   im Intervall [0,2pi)

1.) Definitionsmenge

2.) Nullstellen

3.) Grenzwert, Asymptote, Symmetrien( gerade oder ungerade Funktion)

4.) Maximalpunkte, Minimalpunkte ( erste Ableitung)

5.) Wendepunkte( 2. Ableitung)


Ich habe hier grosse Mühen mit den Punkten 2,4,5 weil man das immer schauen muss wo es gleich 0 ist und ich verstehe nich wie ich herausfinden kann, wo die Nullstellen sind.


Ich danke für eine Hilfe schon im voraus und wünsche einen schönen Tag!

Answer 1

f(x) = SIN(2·x) + 2·COS(x)

1.) Definitionsmenge

D = R

2.) Nullstellen f(x) = 0

SIN(2·x) + 2·COS(x) = 0

Ich vermute nach skizze unten Nullstellen bei pi/2 und 3pi/2

Einsetzen bestätigt die Vermutung.

3.) Grenzwert, Asymptote, Symmetrien(gerade oder ungerade Funktion)

Periodische Funktion. Daher keine Grenzwerte, keine Asymptoten und eine Symmetrie ist auch nicht erkennbar.

4.) Maximalpunkte, Minimalpunkte (erste Ableitung)

2·COS(2·x) - 2·SIN(x) = 0
x = 5/6·pi ∨ x = pi/6 ∨ x = 3/2·pi

f(5/6·pi) = - 3·√3/2
f(pi/6) = 3·√3/2
f(3/2·pi) = 0

5.) Wendepunkte( 2. Ableitung)

- 4·SIN(2·x) - 2·COS(x) = 0

x = 1/2·pi ∨ x = 3/2·pi ∨ x = 2·pi - ATAN(√15/15)

Hier sollten jetzt auch noch die y-Koordinaten berechnet werden.

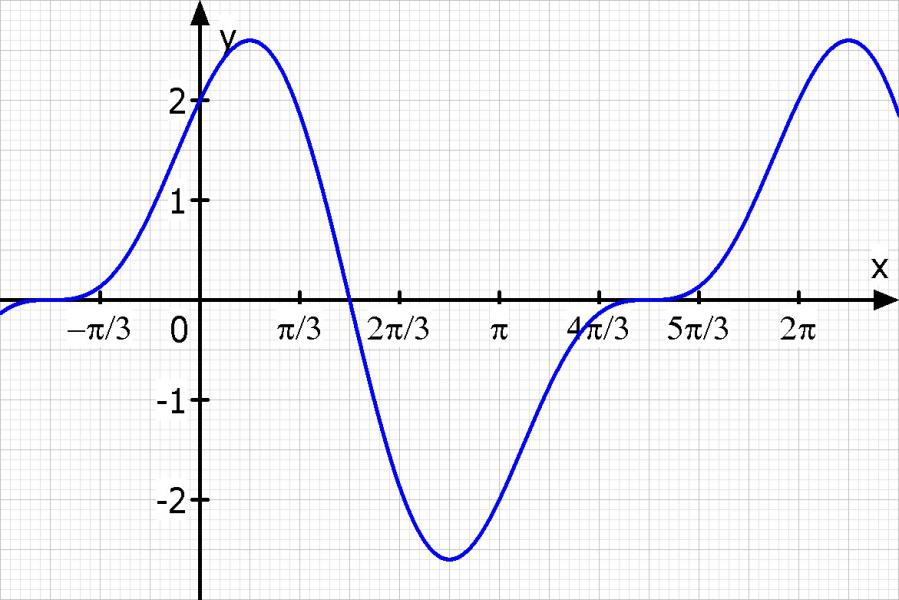
Skizze