sollte in deiner Aufgabenstellung der Definitionsbereich Df = [ 0 ; π/2 ] angegeben sein, dann
1) wäre es nett, wenn du uns in Zukunft so etwas mitteilen würdest
2) kannst du unten bei # weiterlesen (oder aus Interesse auch hier anfangen :-))
f(x) = √cos(x)
Diese Funktionsvorschrift ist nur für cos(x) > 0 definiert, also für x ∈ [ (2k-1) • π/2 ; (2k+1) • π/2 ] mit k∈ℤ.
In diesen Intervallen wiederholen sich die Funktionswerte ständig von Intervall zu Intervall und auch innerhalb der einzelnen Intervalle wiederholen sich die Funktionswerte symmetrisch zur Intervallhälfte.
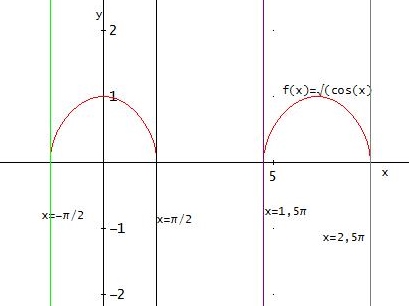
Eine Umkehrfunktion existiert aber nur, wenn die Funktion injektiv ist, wenn also für verschiedene x-Werte aus D auch die Funktionswerte verschieden sind.
Als Definitionsmenge von f musst du also die Hälfte eines der o.g. Intervalle festlegen, z.B. D = [ 0 ; π/2 ] mit k=0
----------------
#
Sei also f: [ 0 ; π/2 ] → ℝ ; f(x) = √cos(x), die Wertemenge von f ist dann W = [0 ; 1]
Für die Berechnung der Funktionsvorschrift von f -1 schreiben wir
y = √cos(x) | 2
nach x auflösen:
y2 = cos(x)
arccos(y2) = x
Variablennamen vertauschen:
y = arccos(x2)
f-1: [0 ; 1] → [ 0 ; π/2 ] ; x ↦ arccos(x2)
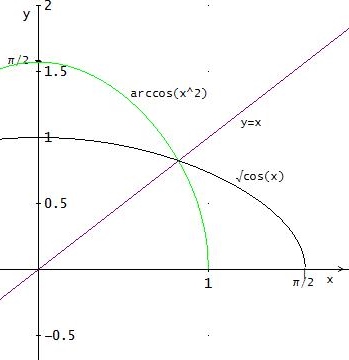
Der Graph einer Umkehrfunktion ergibt sich aus dem Graph einer Funktion durch Spiegelung an der 1. Winkelhalbierenden y = x
Gruß Wolfgang