Funktionsgleichung 3.grades hat in P(0|0) einen Wendepunkt und in Q(-2|2) eine waagerechte Tangente.

Question

ich habe ein Problem, ich habe die Aufgabe bekommen:

Der Graph einer ganzrationalen Funktion 3. Grades hatin P(0|0) einen Wendepunkt und in Q(-2|2) eine waagerechte Tangente. Bestimme die Funktiongleichung dieser Funktion.

bitte helft mir ich bekomm sonst n Nerven zusammenbruch :)

Answer 1

Hi, Deine Funktion ist punktsymmetrisch zum Ursprung (warum?),
verwende daher den Ansatz

f(x) = a*x^3+c*x

und die Bedingungen f(-2)=2 und f'(-2)=0.

Comments

und wie rechne ich das weiter wenn ich die 2 für x einsetzte?

---

Eigentlich schrieb ich "-2".

Die erste Ableitung lautet f'(x) = 3ax^2+c.

Die Bedingungen lauten
f(-2) = 2 ⇒ -8a-2c = 2 und
f'(-2) = 0 ⇒ 12a+c = 0.

Löse dieses Gleichungssystem.

Answer 2

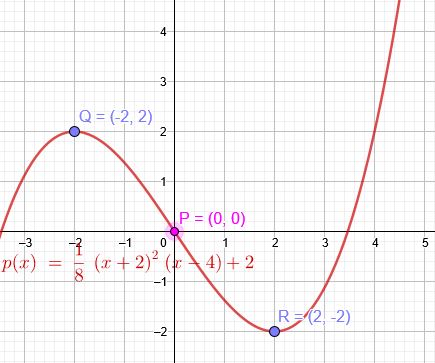
Der Graph einer ganzrationalen Funktion 3. Grades hat in \(P(0|0)\) einen Wendepunkt und in \(Q(-2|2)\) eine waagerechte Tangente. Bestimme die Funktiongleichung dieser Funktion.

Punktsymmetrie in \(P(0|0)\)→\(R(2|-2)\)

↓Verschieben: \(Q(-2|2)\)→ \(Q´(-\red{2}|0)\)

Nullstellenform der kubischen Parabel:

\(f(x)=a(x+\red{2})^2(x-N)\)

↓Verschieben:\(R(2|-2)\)→\(R´(2|-4)\):

\(f(2)=a(2+2)^2(2-N)=16a(2-N)\)

\(16a(2-N)=-4\) →\(16a(N-2)=4\)   →\(4a(N-2)=1\)   → \(a=\frac{1}{4N-8}\)

\(f(x)=\frac{1}{4N-8}(x+2)^2(x-N)\)

↓Verschieben:\(P(0|0)\)→\(P´(0|-2)\)

\(f(0)=\frac{1}{4N-8}(0+2)^2(0-N)=\frac{1}{4N-8}\cdot (-4N)\)

\(\frac{1}{4N-8}\cdot (-4N)=-2\)      \(N=4\)     \(a=\frac{1}{8}\)

\(f(x)=\frac{1}{8}(x+2)^2(x-4)\)

↑Verschieben:  \(p(x)=\frac{1}{8}(x+2)^2(x-4)+2\)