Funktionsgleichung 3.grades hat in P(0|0) einen Wendepunkt und in Q(-2|2) eine waagerechte Tangente.

Question

ich habe ein Problem, ich habe die Aufgabe bekommen:

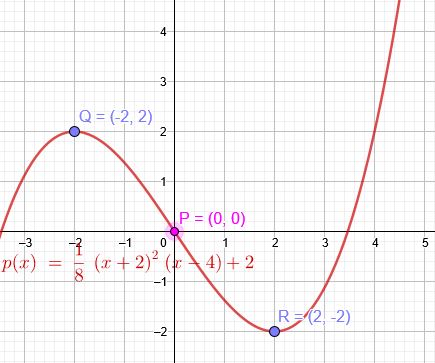
Der Graph einer ganzrationalen Funktion 3. Grades hatin P(0|0) einen Wendepunkt und in Q(-2|2) eine waagerechte Tangente. Bestimme die Funktiongleichung dieser Funktion.

bitte helft mir ich bekomm sonst n Nerven zusammenbruch :)

Answer 1

Hi, Deine Funktion ist punktsymmetrisch zum Ursprung (warum?),
verwende daher den Ansatz

f(x) = a*x^3+c*x

und die Bedingungen f(-2)=2 und f'(-2)=0.

Comments

und wie rechne ich das weiter wenn ich die 2 für x einsetzte?

---

Eigentlich schrieb ich "-2".

Die erste Ableitung lautet f'(x) = 3ax^2+c.

Die Bedingungen lauten
f(-2) = 2 ⇒ -8a-2c = 2 und
f'(-2) = 0 ⇒ 12a+c = 0.

Löse dieses Gleichungssystem.