Ist zwar schon fünf Jahre her, aber hier ist die Antwort:
Du hast recht mit der Herleitung, dass
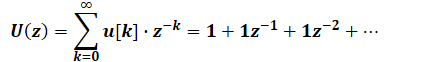
Text erkannt:
\( U(z)=\sum \limits_{k=0}^{\infty} u[k] \cdot z^{-k}=1+1 z^{-1}+1 z^{-2}+\cdots \)
ist. Aber wie kommt man jetzt auf die richtige Lösung?
Schritt 1: Wir nennen deine Lösung einfach mal "A":
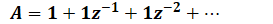
Text erkannt:
\( A=1+1 z^{-1}+1 z^{-2}+\cdots \)
Schritt 2: Wir berechnen "A-1", auch wenn das vielleicht erstmal komisch wirkt, Aber vertrau mir :)

Text erkannt:
\( A-1=1 z^{-1}+1 z^{-2}+\cdots \)
Schritt 3: Wir teilen beide Seiten durch z^(-1). Wirkt auch seltsam, aber lass mal schauen was passiert:
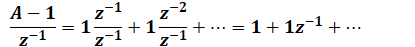
Text erkannt:
\( \frac{A-1}{z^{-1}}=1 \frac{z^{-1}}{z^{-1}}+1 \frac{z^{-2}}{z^{-1}}+\cdots=1+1 z^{-1}+\cdots \)
Fällt dir was auf? Die rechte Seite der Gleichung ist auf einmal genau gleich A!
Wir erhalten also die Gleichung:
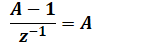
Text erkannt:
\( \frac{A-1}{z^{-1}}=A \)
Und wenn wir das umformen, kommt raus:
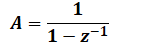
Text erkannt:
\( A=\frac{1}{1-z^{-1}} \)
Und wir haben unsere Lösung.
und viel Glück!
Text erkannt:
\( \frac{A-1}{z^{-1}}=1 \frac{z^{-1}}{z^{-1}}+1 \frac{z^{-2}}{z^{-1}}+\cdots \)
Text erkannt:
\( X_{A}(z)=\sum \limits_{k=0}^{\infty} x[k] \cdot z^{-k} \)