Aufgabe "Produktion"
Ein Betrieb stellt drei verschiedene Endprodukte E1, E2 und E2 her und verwendet dafür drei Rohstoffe R1, R2 nd R3. Dabei werden für die Herstellung von 1 ME der Sorte E1 4 ME Rohstoffe der Sorte R1, 8 ME der Sorte R2 und 8 ME der Sorte R3 benötigt. Die entsprechenden Mengen sind (2, 6, 4) für E2 und (8, 10, 8) für E3.
a) Fassen Sie die oben stehenden Rohstoffwerte in der folgenden Tabelle zusammen:
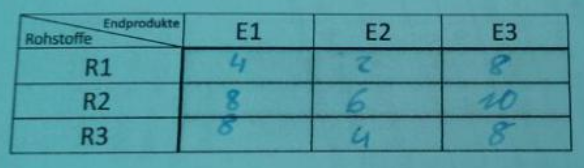
b) Erstellen Sie einen Gozintographen (Verflechtungsdiagramm) zu der Tabelle in Aufgabe a).
c) Bestimmen Sie, wie viele Rohstoffe für die Produktion von 50 ME der Sorte E1, 100 ME der Sorte E" und 60 ME der Sorte E3 benötigt werden.
d) Zum Ende des Jahres sol möglichst der gesamte restliche Lagerbestand von 54 ME der Sorte R1, 84 ME der Sorte R2 und 68 ME der Sorte R3 verbraucht werden. Prüfen Sie, ob dies möglich ist und bestimmen Sie gegebenenfalls die Mengen an Endprodukten E1, E2 und E3, die aus diesen Lagerresten hergestellt werden können.
a) bis c) hab ich hinbekommen wie ist aber d) zu lösen :( ?