Verteilungsfunktion bestimmen

Question

ich habe eine Frage zur Bestimmung der Verteilungsfunktion, vielleicht könnt ihr mir hier ja helfen.

Es handelt sich dabei um die folgende Aufgabe:

Bis auf den Teil d ist das ja auch kein Hexenwerk. Aber selbst mit Lösung komme ich bei der d leider nicht weiter. Die Lösung lautet:

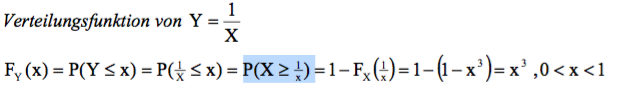
Ich komme bist vor die blau Markierung. Die Frage ist nun wie komme ich auf die blaue Markierung? Und wie geht es dann weiter?

Answer 1

für reelle Zahlen \(x,X >0 \) sind folgende Umformungen äquivalent:

$$ \frac{1}{X} \leq x $$

$$ 1 \leq xX $$

$$ \frac{1}{x} \leq X $$

Gruß

Comments

Hm, kannst du mir das vielleicht noch etwas näher erklären? Ich glaube ich verstehe jetzt nicht ganz was mit dem großen X und dem kleinen x gemeint ist...

Vielen Dank

Gruß

---

Du willst doch wissen wann die Zufallsvariable \(\frac{1}{X}\) kleiner gleich einem Wert \(x\) (schlechte Variablenwahl, da gleicher Buchstabe und der Unterschied nur durch Groß- und Kleinschreibung) und durch die obige Umformung (unter den gegebenen Voraussetzungen) ist das genau dann wenn \(X\) größer gleich dem Kehrwert des Wertes von \(x\) ist.

---

Ach klar... jetzt wo du s sagst. Habe mir das ganze gerade mal mit anderen Variablen aufgeschrieben, dann ist es sofort klar.
Kannst du mir auch noch bei den nächsten Schritten helfen? Da weiß ich auch noch nicht wie ich da vorgehen muss...
Danke

Gruß

---

Wo genau ist dort die Schwierigkeit? Wenn du die Verteilungsfunktion schon bestimmt hast musst du nur noch einsetzen. \(P(X \geq a)\) ist das Gegenereignis zu \(P(X<a)\).

---

Hm, schwierig zu beschreiben, aber ich bin mir nicht sicher wie ich auf

1-(1-x^3)

komme...

Da irgendwo hänge ich leider...

---

Für \(t \geq 1\): \(F_X(t) = 1-t^{-3} \). Da \(\frac{1}{x} \geq 1\):

$$ F_X(\frac{1}{x}) = 1 - \left( \frac{1}{x} \right)^{-3} = 1 -x^3$$

Am besten mal Potenzgesetze wiederholen.