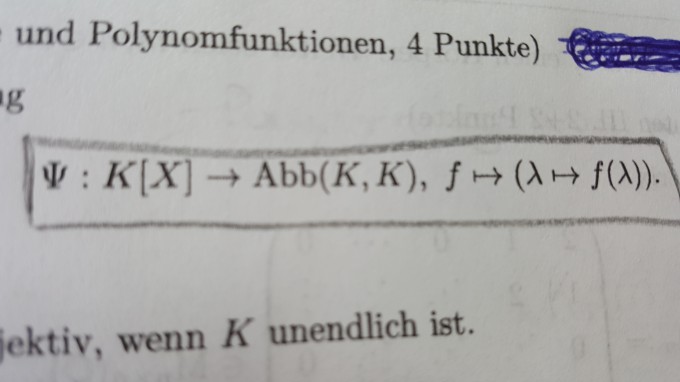Polynome und Polynomfunktion

Question

kann mir jemand bei dieser Aufgabe bitte helfen.

Also es ist diese Abbildung gegeben und ich soll bei 

a) zeigen,  dass diese Abbildung injektiv ist, wenn K unendlich ist. 

b) ist genau dann surjektiv, wenn K endlich ist. 

Mein Ansatz bei a ist, dass man den Kern der Abbildung  zeigt um damit die Injektivität zeigt. Aber ich komme nicht weiter wie ich das machen soll. Kann mir bitte jemand helfen.  :o 

Comments

Ist Lambda fest und / oder vorgegeben? 

---

nein, λ ist weder fest noch vorgegeben

Answer 1

Die Abbildung \(\Psi\) ordnet jedem \(f(X)\in K[X]\) die Abbildung \(\lambda\mapsto f(\lambda)\) zu. Die Frage ist also, ob zwei verschiedene Polynome dieselbe Funktion erzeugen koennen. Dazu koenntest Du den Identitaetssatz für Polynome (eigentlich Polynomfunktionen) aus der Analysis nachschlagen. Musst dir dann nur noch ueberlegen, warum der nur dann funktioniert, wenn \(K\) unendlich viele Elemente hat.

Beim zweiten Teil kannst Du mit Polynominterpolation argumentieren.