Welche reellen Lösungen besitzt folgende Betragsgleichung: |x²+2x-1|=|x|

Question

wie schon oben gefragt , bin ich mir bei der Aufstellung der Fälle bzw. der Intervalle, sowie der Lösung sehr unsicher.  Allgmein gibt es doch bei zwei Beträgen 3 Fälle : Beide Terme zwischen den Betragstrichen sind positiv; beide Terme sind negativ und ein Term ist positiv der andere jedoch negativ, richtig ? Hier die Gleichung :

|x²+2x-1|=|x|

Comments

Es langt, zwei Fälle zu unterscheiden:
(1)  x² + 2x - 1 = x
(2)  x² + 2x - 1 = -x.

---

Leider nein , denn erst durch den 4. Fall : x<0 u. x²+2x-1<0 kommt man auf die Lösung der Betragsgleichung...

---

Die Betragsgleichung hat vier Lösungen.

Answer 1

|x²+2x-1|=|x|

1. Fall    x≥0 und    x²+2x-1 ≥0

dann     x²+2x-1= x

               x²+x-1= 0

              x =   (-1 ±√5 ) / 2 einer ist negativ, also höchstens

               x =   (-1 + √5 ) / 2   passt, da ist auch    x²+2x-1 ≥0

2. Fall  

               x²+2x-1= - x

            x^2 + 3x - 1 = 0

            gibt x = ( -3 ±√13 ) / 2   der positive fällt weg, also

            x = ( -3  - √13 ) / 2 

passt denn auch hier    x²+2x-1 ≥0

3.  Fall        x≥ 0 und    x²+2x-1 < 0   etc..

4. Fall        x< 0 und    x²+2x-1 < 0

Answer 2

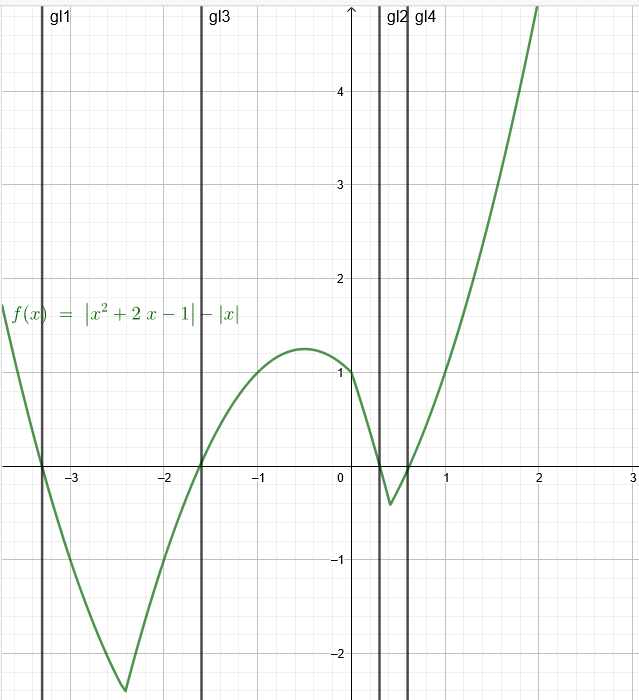
|x²+2x-1|=|x|

\( \sqrt{(x²+2x-1)^2} \)=\( \sqrt{x^2} \)|^2

(x²+2x-1)^2=x^2

(x²+2x-1)^2-x^2=0

[x²+2x-1+x]*[x²+2x-1-x]=0

1.)x²+3x-1=0

x₁≈-3,3       Kontrolle:  |(-3,3) ²+2*(-3,3) -1|=|-3,3  |    stimmt

x₂≈0,3      Kontrolle: |(0,3) ²+2*(0,3) -1|=|0,3  |   stimmt

2.) x²+x-1=0

x₃≈-1,6     Kontrolle: |(-1,6) ²+2*(-1,6) -1|=|-1,6  |   stimmt

x₄≈0,6       Kontrolle: |(0,6 ) ²+2*(0,6 ) -1|=|0,6   |   stimmt