Stellen sie die Menge x als Funktion des Preises p dar:
Gleichung für p = p(x) nach x umstellen:
p = 1/8 * (1296-x)3/4 | • 8 |4/3 | - 1296 | • (-1) | 0,16 ausklammern | ↔
x(p) = 0, 16 · ( 81 - p4/3 )
Bei welchem Preis p* und welcher Menge x* wird der Erlös maximal ?
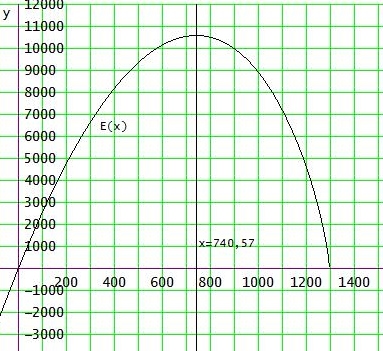
E(x) = x • p(x) = 1/8 • x • (1296 - x)3/4
Das Maximum von E(x) berechnet man mit der Ableitung E'(x)
Produktregel und Potenzregel ergibt:
E'(x) = (1296 - x)3/4 / 8 - 3·x / [ 32·(1296 - x)1/4 ]
E'(x) = 0 | • ( 32·(1296 - x)1/4 )
......
→ x = 5184 / 7 ≈ 740,57 mit VZW von + → -
Erlösmaximale Menge = xmax = 740,57 Mengeneinheiten
p(xmax) ≈ 14,30 (Geldeinheiten)
Gruß Wolfgang