Erläutern Sie den Begriff Stammfunkion!
Ist F: D→ℝ differenzierbar mit F' = f , dann heißt F "Stammfunktion" von f .
gesuchte Fläche:
Schnittstellen der beiden Funktionen:
x2 + 4 = 2x2 - 8 ⇔ x = - 2·√3 oder x = 2·√3
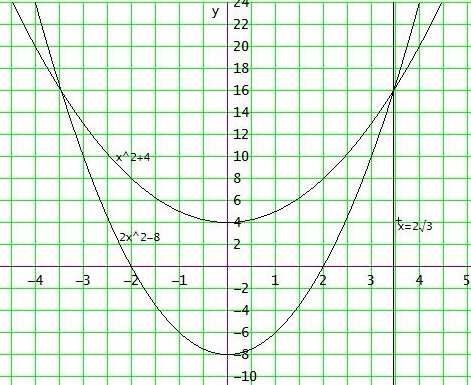
in diesem Bereich liegt x ↦ x2 + 4 höher und wegen der Symmetrie zum Ursprung kann den doppelten eingeschlossenendoppeltenFlächeninhalt über dem Intervall [0 ; 2√3] ausrechnen:
A = 2 • 0∫2√3 (x2+4 - (2x2 -8)) dx = 2 • 0∫2√3 (12-x2) dx = 32 • √3
Rotationsvolumen:
die Überlegungszeichnung ist sehr gewöhnungsbedürfitig.
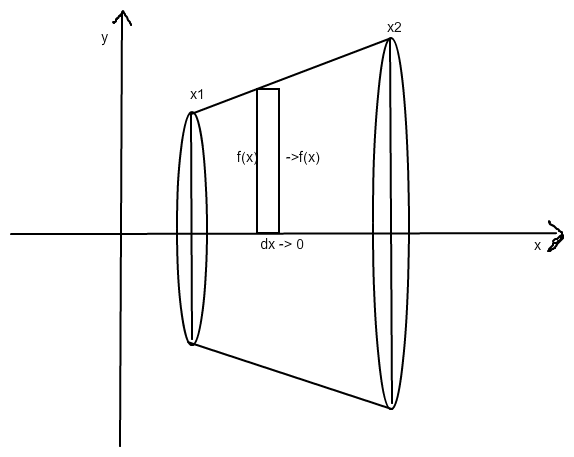
Du musst dir das kleine Rechteck in der Mitte so schmal [ Δx sehr klein ≈ dx ] vorstellen, dass die beiden senkrechten Seiten "praktisch" gleich lang [ ≈ f(xi) ] sind und oben bis zum Graph und unten bis zur x-Achse reichen. Wenn dieses Rechteck um die x-Achse rotiert, entsteht ein Zylnder mit der Höhe Δx ≈ dx und dem Radius f(xi). Dieser hat das Volumen π • r2 • h = π • f(xi)2 • dx.
Addiert man diese "beliebig vielen" kleinen Zylinder ergibt ihre Summe ∫ π • f(x)2 • dx.
→ Rotationsvolumen = π • x1∫x2 f(x)2 • dx.
Gruß Wolfgang