Bestimmen einer Taylorreihe der Funktion f(x) = 1/(x^2- 4x + 3) um x=2

Question

!
Ich habe hier eine Aufgabe, von der ich nicht weiss, wie ich sie anpacken soll.

Es ist eine Altklausuraufgabe.

"Bestimmen Sie die Taylorreihe von

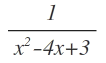
um den x₀= 2 und geben sie den Konvergenzradius an"

Mir ist klar, dass ich diese Formel bis zu 4x Ableiten müsste, um am Ende an eine Reihe zu kommen.

Meine Fragen:
> MUSS ich sie wirklich 4x ableiten (oder wie oft?) oder gibt es da einen schnelleren Weg um solche Aufgaben zu bearbeiten?
> Muss das Endergebnis immer mit einem Summenzeichen angegeben werden?
  Oder genügt hier auch eine gewisse Anzahl von Polynomen, je nach dem wie oft abgeleitet wurde?
> Wie sieht ein Konvergenzradius bei solch einer Aufgabe aus?

Comments

x^2 - 4x + 3 = x^2 - 4x + 4 - 4 + 3 = (x-2)^2 - 1

Nun würde ich nach einer schlauen Substitution suchen.

Aber, ob das ein schneller Weg ist?

---

fehlt da nicht noch +3 im Nenner ???

---

Richtig. Danke. Dann wird's einfacher. Ich habe das oben korrigiert.

Answer 1

1 / ( x^2 -4x + 3 ) substituieren x = z+2  ( dann ist der Entwicklungspunkt für z schon mal z=0)

1 / (z^2 - 1)  =   -1 / ( 1 - z^2 )   das passt zur geometrischen Reihe mit q = z^2

also   -1 / ( 1 - z^2 )    =  -  Summe k=0 bis ∞ über   z^2k 

jetzt Substitution rückwärts

-1 / ( 1 - (x-2)^2  )    =    -  Summe k=0 bis ∞ über   (x-2)^2k 

                                  =    Summe k=0 bis ∞ über   - (x - 2 )^2k 

und das konvergiert für z^2 < 1   also ist der Konv.radius = 1 .

 

Comments

Vielen Dank für die Antwort. Auf diese Idee wäre ich nie gekommen!

Aber noch eine Frage zu deinem zweiten Schritt.
Ersetzt du hier x duch z+2 oder ersetzt du den kompletten Nenner djurch z+2,
mir ist nicht so ganz ersichtlich, wie du plötzlich auf 1/(z²-1) kommst.

---

1/((x-2)² - 1 ) =1/(z^2-1) =  -1/((1-z^2) = (-1)*1/(1-z^2) 

z = x-2 ist dasselbe wie x = z+2.