Anzahl Möglichkeiten, eine 12x13-Matrix mit Quadraten zu befüllen, die an mindestens einer Kante zusammenhängen?

Question

Wieviele Möglichkeiten gibt es eine 12 x 13 Matrix mit Figuren aus drei Quadraten zu befüllen, die an mindestens einer Kante zusammenhängen?

Möchte man aus drei Quadraten Figuren legen, die an mindestens einer Kante zusammenhängen, entstehen diese zwei Figuren:

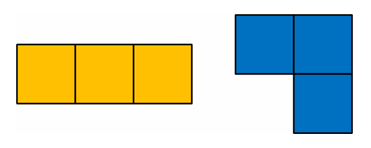
Diese Figuren können natürlich gedreht und gespiegelt werden. Dann entstehen quasi sechs verschiedene Figuren. Hier zum Ausmalen, Ausschneiden und Ausprobieren:

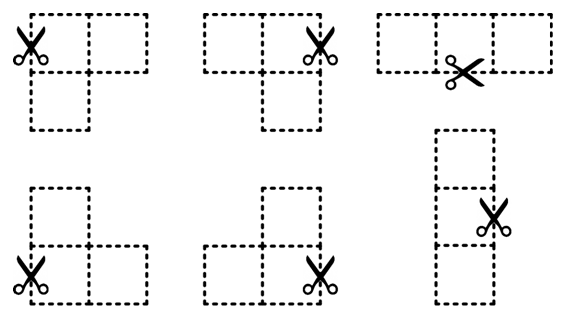
Das Bild kann beliebig oft ausgedruckt und ausgemalt werden. Begrenzt ist die Anzahl durch deinen Drucker, deinen Papiervorrat und deine Buntstifte.

Eine Matrix mit m Zeilen und n Spalten, wobei m oder n durch drei teilbar ist, kann vollständig mit den oben dargestellten Figuren ausgefüllt werden.

Hier ein Beispiel:

Bei einer 3x3-Matrix

gibt es 10 Möglichkeiten die Matrix mit den oben genannten Figuren zu befüllen:

Noch ein Beispiel:

Bei einer 3x4-Matrix

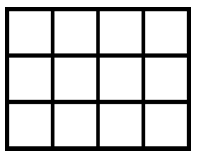
gibt es 23 Möglichkeiten die Matrix mit den oben genannten Figuren zu befüllen:

Und noch ein Beispiel:

Bei einer 3x5-Matrix

gibt es 62 Möglichkeiten die Matrix mit den oben genannten Figuren zu befüllen.

Jetzt endlich zur Aufgabe:

Wieviele Möglichkeiten gibt es eine 12x13-Matrix zu befüllen?

Answer 1

Antwort gelöscht

(Sorry, hatte das Word-Dokument zu spät gelesen und "rein kombinatorisch" geantwortet)

Comments

Das Problem scheint doch etwas umfangreicher zu sein...

Ich hoffe es ist überhaupt lösbar!

---

Man kann mit Sicherheit ein Programm schreiben, das die Möglichkeiten zählt :-)

---

Also doch etwas programmieren...
Ich glaube da bin ich raus.

Vielen Dank schon mal für die Bemühungen!

---

Wollte damit nicht sagen, dass man es nicht auch anders lösen kann.

Würde mich auch interessieren!

---

Versuche mal die 12*13 matrix aus den gegebenen matrizen zusammenzubauen. DIe Gesamtkombination hat also dann als Gesamtmöglichkeiten das Produkt der Einzelmöglichkeiten.

---

Den Lösungsweg habe ich schon versucht. Komme aber über eine Matrix von 12x12 nicht hinaus. Bleibt quasi ein "Rest" über...

---

Mir ist noch was aufgefallen: Die Anzahl der Möglichkeiten steigt von der 3x3 Matrix zur 3x4 Matrix um 13 , von der 3x4 zur 35 Matrix um 39, also 13*3. Das ist vielleicht Zufall, aber meine Vermutung wäre, dass bei einer 3x6 Matrix die Anzahl der Möglichkeiten 62+39*3=179 ist. Das könnte man vielleicht mit Induktion versuchen zu beweisen. Dann hätte man schonmal die Lösung für eine 3*13 Matrix hergeleitet.

---

Ich habe erhebliche Zweifel, dass sich bei größeren Matrizen jede Lösung in rechteckige Teilblöcke zerlegen lässt.

---

Das hört sich schon mal gut an.

Da die Aufgabe ja vorgibt, dass `m oder n (im gesuchten Fall 12 oder 13) durch drei teilbar ist und das ist ja gegeben, bin ich mir Sicher, dass es eine Lösung gibt.

---

Demnach würde man bei einer Matrix von 3x13 auf 56885 kommen. Wenn ich auf die schnelle richtig gerechnet habe...

---

Ich habs mal nachgerechnet, ich komme auf N_3x13=10+13*∑⁹_i=1 3ⁱ =383822 :). Und um dann eine 12x13 Matrix zu bauen ist dann N_12x13=4* N_3*13  =1535288.

---

Da scheint mir irgendetwas nicht berücksichtigt wurden zu sein. (siehe für die genaue Aufgabe auch das Word-Dokument)

Wenn man bei der 3x13 Matrix schon 383822 Möglichkeiten hat sollten es doch bei der 12x13 Matrix wesentlich mehr als 1535288 sein.

Hier muss sich eventuell doch der Computer um das Poblem "kümmern". Allerdings reichen meine einfachen Programmierkenntnisse nicht aus...

Danke schon mal an alle die sich mit der Lösung des Problems beschäftigen. Eventuell hat ja noch jemand die zündende Idee.

Grüße Jochen

---

Hi,

Ja, ich hab nen Fehler gemacht:  N_12x13= (N_3*13)^{4  ,}aber das wird ein riesiges Ergebnis. 

Gruß

 

---

Da es ja auch eine vielzahl an Möglichkeiten gibt, ist eine recht große Zahl wahrscheinlich!

Wie stellt sich das Ergebnis dar?

---

DIe Gesamtanzahl ist die Anzahl der Möglichkeiten der großen Matrix der einzelnen kleineren Matrizen miteinander multipliziert. 

N_12x13=383822⁴= 2.1702984*10²²

 

---

Es wären dann 21702984000000000000000 Möglichkeiten.

Da wird mir leider gesagt: Die Antwort ist falsch...

Aber ich bin der Meinung, dass sich die Zahl in diesem Zahlenraum bewegt.

---

In "The Art of Programming" von Donald Knuth werden so ähnliche Probleme behandelt. Da geht es darum, wie man zu einem effizienten Algorithmus kommt bzw. mit welchem Algorithmus man solche Probleme überhaupt lösen kann.
Kann irgendwer algorithmisch beschreiben, wie man vorgehen müsste oder das Problem irgendwie umformulieren, dass man es mit den Datentypen einer normalen Programmiersprache bearbeiten kann?

---

Hat schon jemand eine Lösung? Das hört sich gar nicht so schwer an.

Man kann das Problem Problem umformulieren in das "Problem der exakten Überdeckung."
https://en.wikipedia.org/wiki/Exact_cover

Dieses wiederum kann man mit dem Algorithmus "Dancing Links" mit verhältnismäßig wenig Aufwand lösen.
https://en.wikipedia.org/wiki/Dancing_Links

Der Algorithmus verdankt übrigens Donald Knuth seinen Namen. Warum auch immer. Entdeckt haben den Algorithmus Hirosi Hitotumatu und Kohei Noshitaschon im Jahr 1979.

Möglicherweise ist ein Matheforum nicht der richtige Ansprechpartner, sondern eher ein Programmiererforum.