Rotationskörper zeichnen

Question

Aufgabe:

Der Ausdruck \[ V=\pi \int \limits_{0}^{4}\left(4-\frac{1}{2} x\right)^{2} d x \] liefert den Inhalt eines Rotationskörpers. Er entsteht, wenn der Graph der linearen Funktion \( f \) mit \( f(x)=4-\frac{1}{2} x \) uber dem Intervall \( [0 ; 4] \) um die x-Achse rotiert. Der Körper ist Teil eines Kegels (Kegelstumpf).

Skizze:

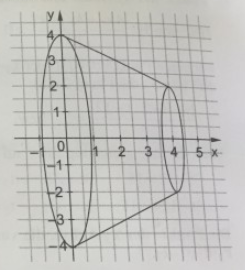
Die Aufgabe ist es, den Rotationskörper mit der Funktion, die ihr im Bild sehen könnt zu zeichnen. Ich habe die Gerade gezeichnet und weil sie ja rotiert, an der x-Achse gespiegelt. Nur woher weiß ich die Größe des Kreises?

Comments

Es ist ja schon gezeichnet.

Bei x = 0 ist der Radius 4 und bei x = 4 ist der Radius 2.

---

Ja, aber warum?

---

Das ist eine Skizze wie im Zeichenunterricht, wenn du einen Blumentopf oder eine Vase zeichnen musst.

Nur zeichnest du dort in der Regel mit der y-Achse als Rotationsachse.

Answer 1

Die Breite der Ellipsen wird pi mal Daumen so gewählt das man es sich vorstellen kann.

Die Höhe der Ellipsen ist ja durch den Funktionswert an der Stelle vorgegeben.

Hier mal als 3D-Darstellung via Geoknecht 3D.

Comments

x- und y-Achse sind in Geoknecht falsch beschriftet . Tut aber der Vorstellung keinen Abbruch.

Mein Versuch mit Eingabe:

zylinder(0|2|-2 4|4|2|20)[0 90 0]
koordinatenebenen(xy yz#)

ist aber noch nicht mal um die x-Achse zentriert.

---

Nein, die Achsen sind im Allgmeinen richtig beschriftet mit x (horizontal) | y (vertikal) | z (Höhe). Es gibt aber auch andere Varianten.

Für die Aufgabe habe ich den Zylinder tatsächlich Richtung y-Achse gedreht, er muss aber Richung x-Achse. Hier ist die korrigierte Version.