fk(t)= k*(t-15)*e-0,01t+k*15
k=20 ergibt f(t) = 20 • (t-15) • e-0,01·t + 300
zu lösen ist erst einmal die Gleichung 20 • (t-15) • e-0,01·t + 300 = 450
Durch Einsetzen in die Intervalle zwischen den Lösungen kann man dann feststellen, wo f(t) > 450 gilt
20 • (t-15) • e-0,01·t + 300 - 450 = 0
diese Gleichung kannst du wohl kaum explizit nach x auflösen.
Man benutzt dann ein numerisches Näherungsverfahren, zum Beispiel das
Newtonverfahren:
g(t) = 20 • (t-15) • e-0,01·t + 300 - 450
Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben (oder mit Hilfe eines Plotters), berechnet man immer bessere Werte mit der Formel
xneu = xalt - g(xalt) / g ' (xalt)
Eine Lösung ist: t ≈ 24.59087133
Der Plotter gibt eine zweite Lösung her, die du mit dem Startwert 375 genauer berechnen kannst:
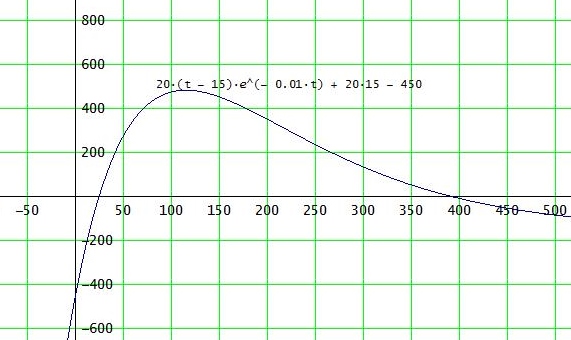
Infos dazu findest du hier:
https://de.wikipedia.org/wiki/Newton-Verfahren
Gruß Wolfgang