> Und wie kann man das Verhalten im Unendlichen Interpretieren?
das Verhalten einer gebrochenrationalen Funktion erkennt am genauesten, wenn man ihre Asymptote betrachtet:
Mit der Polynomdivision (ax2 + 5) : (3x-1) erhält man
\(\frac{ax^2+5}{3x-1}\) = a/3 • x + \(\frac{a/3 + 5}{3x-1}\)
Da der Rest für x→±∞ gegen 0 strebt, nähert sich der Graph von f für x→±∞ immer mehr dem Graph der Asymptotenfunktion.
Also:
limx→∞ fa(x) = limx→∞ (a/3 • x) = ∞ für a≥0
limx→∞ fa(x) = limx→∞ (a/3 • x) = - ∞ für a<0
Für a=2 hier ein Plotterbild:
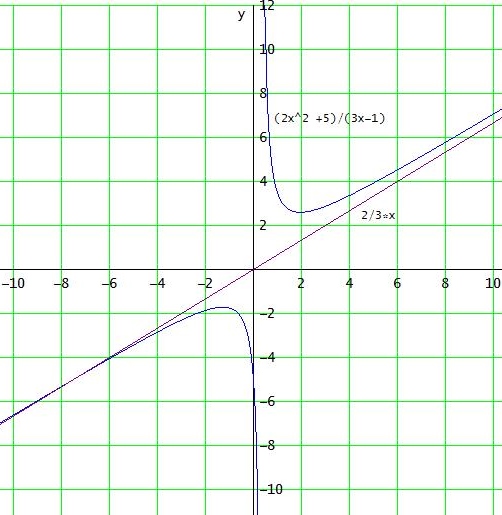
Gruß Wolfgang