Deine Nachfragen zeigen, dass Du weder den LINK angeklickt hast
{also wie die exakte Lösung mit der Umkehrfunktion von x*e^x
die ja LambertW(n,x) lautet}
noch die Potenzgesetze zu kennen scheinst...
§1) a^u * a^v = a^{u+v}
§2) um nach x aufzulösen gibt es 3 Wege:
a) exakte Umstellung per Umkehrfunktion
(da Ihr LambertW nicht hattet, bin ich nicht näher drauf eingegangen)
b) Substitution mit Erkennung primitiver Grundrechenarten
(was ich bereits hingeschrieben hatte)
c) Näherungslösungen wie Bisektion oder Newton-Iteration
(hattet Ihr das schon?)
http://www.gerdlamprecht.de/Roemisch_JAVA.htm
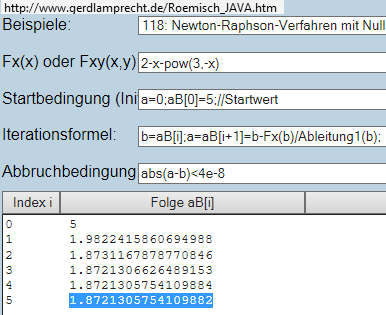
Beispiel 118 bei Fx(x) eingeben: 2-x-pow(3,-x)
und der spuckt die 2. reelle Lösung aus:
Um logisch an die Sache heranzugehen, schreibt man die gegebenen Daten auf:
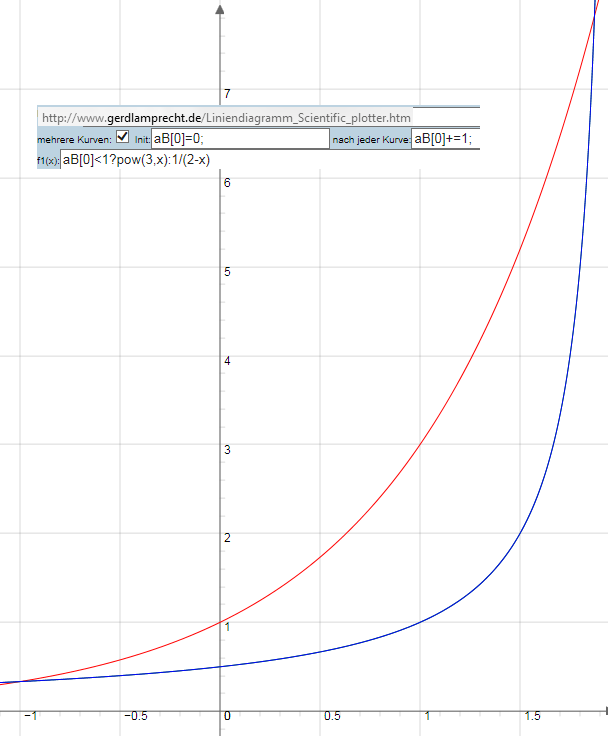
gegeben: f1(x)= 3^x
f2(x)=1/(2-x)
gesucht: x, wenn f1(x)=f2(x) -> Damit also der Schnittpunkt [ x , f1(x) ]
Lösung b):
um die x'e links & rechts des Gleichheitszeichens zu vereinfachen, gibt es die
Substitution: man will Klammern vereinfachen und die Potenz so einfach wie möglich haben
2-x = 3^-x | *3² um §1 rechts der Klammer anwenden zu können, denn u=-x und v=2
3²*(2-x)=3^[2-x] | jetzt gibt es links & rechts der Klammer identische Teile für Subst.
u=2-x; x=2-u ergibt
3²*u = 3^u
3*3*u = 3^u = Produkt[3*3*..*3] u mal multiplizieren
Nun sollte selbst ein Schüler der 6. Klasse erkennen, dass die rechte Seite gleich der linken Seite ist,
wenn man 3 mal die 3 mit einander multipliziert, denn
3*3*3 = 3*3*3
u=3
Rücksubst: x = 2-u=2-3=-1
y = f1(x) = f1(-1) = 3^-1 = 1/3
Endergebnis: Schnittpunkt= [x,y]=[-1 , 1/3]
exakte Lösung a)
x[n]=(LambertW(n,-(log(3))/9)+2 log(3))/log(3),n=-2...1
der LINK zeigt zum Rechner, der neben WolframAlpha die Funktionswerte von
-(log(3))/9=-0.1220680320742344101550272485469473... kann
von den 4 Lösungen suche ich mal die erste reelle heraus (also ohne komplexen Anteil)
die auch mit Lösung b) übereinstimmt: n=-1
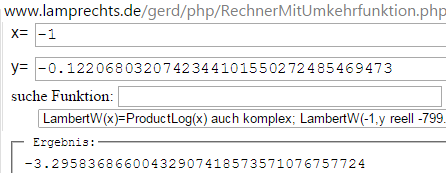
x[-1]=(-3.29583686600432907418573571076757724+2 log(3))/log(3)= -1
Alle 4 Lösungen zusammen:
n | x[n]
-2 | -1.85885965617089619104320394170070-6.671690431844623856155953086257 i
-1 | -1.00000000000000000000000000000000
0 | 1.872130575410988181375709728204236
1 | -1.85885965617089619104320394170070+6.671690431844623856155953086257 i
Plot (den Ihr vermutlich nur grob ablesen solltet) bestätigt die beiden reellen Schnittpunkte: