1) Antwort 1
2)
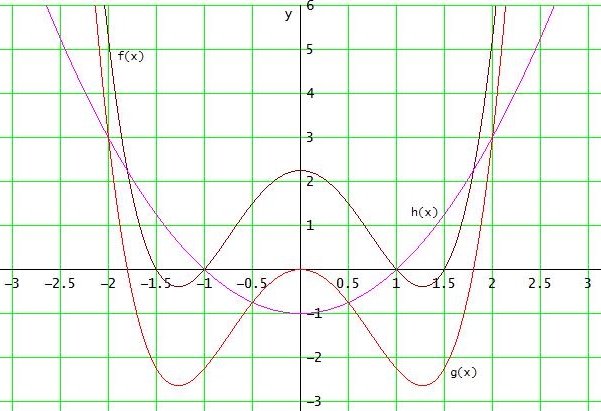
f(x) = x4-3,25 x2 + 2,25 (nehme ich an)
f(-x) = (-x)4 - 3,25 (-x)2 + 2,25 = x4-3,25 x2 + 2,25 = f(x) für alle x∈D
→ f ist symmetrisch zur y-Achse
3)
f(-2) = 5,25 P ja
f(0,5) = 1,5 Q nein
4) ??
5)
f '(x) = 4x3 - 6,5x = 0 ergibt Extremstellen
⇔ 4x • ( x2 -- 1,625) = 0
⇔ x = 0 oder x = ±√1,625 ≈ 0,,3187
f(0) = 2,25 → H(0 | 2,25)
wegen der W-Form des Graphen ergeben sich "genau 3 Nullstellen" nur, wenn der Hochpunkt (0|2,25) auf der x-Achse liegt, also bei einer Verschiebung um 2,25 nach unten
g(x) = x4- 3,25 x2
6)
x4 - 3,25 x2 + 2,25 = x2 -1
x4 - 4,25 x2 + 3,25 = 0
setze z = x2
z2 -4,25 z + 3,25 = 0
z2 + pz + q = 0
pq-Formel: p = -4,25 ; q = 3,25
z1,2 = - p/2 ± \(\sqrt{(p/2)^2 - q}\)
...
z1 = 13/4 ; z2 = 1
x2 = 13/4 → x1,2 = ± √13 / 2 ≈ 1,8
x2 = 1 → x3,4 = ± 1
7)
h2(x) = (x - 1)2 - 1
8)
Die Gerade durch den Punkt P( xp | yp ) mit der Steigung m hat die Gleichung
y = m • ( x - xp ) + yp [ Punkt-Steigungs-Formel ]
m = (0 - (-1) / (1-0) = 1
y = (x - 1) + 0
y = x-1 (kannst du auch einfach einer Zeichnung entnehmen)
Gruß Wolfgang