Tangentengleichung aufstellen mit einem Punkt

Question

Gegeben ist die Funktion f(x)=-1/2x²+2x+2 

a)

eine gerade durch den Punkt P(-1/0) schneidet den Graphen von f an der Stelle x=3

Geben sie die Geradengleichung und die Größe des Schnittwinkels an.

b)

Welche gerade durch den Punkt P(-1/0) ist tangente an den Graphen von f

Habe große Schwierigkeiten 

Bitte mit erklärtem Rechenweg.

Comments

Du siehst  hier die Funktion f (nach unten geöffneter Graph) und die beiden Geraden a und b entsprechend den Aufgaben a) und b).

---

Danke, 

Und wie berechne ich das ?

---

vgl. meine Antwort

Answer 1

f(x)=-1/2x²+2x+2 

f '(x) = -x + 2

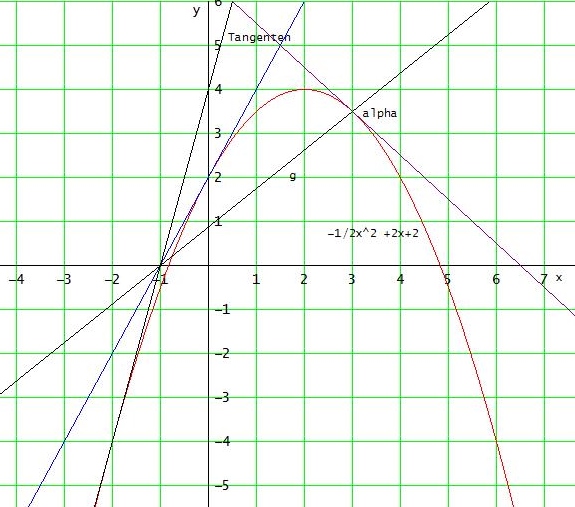
a)

f (3) = 7/2, die Gerade verläuft also durch P( -1 | 0) und durch S(3 | 3,5)

→ ihre Steigung m_G = (3,5 - 0) / (3 - (-1)) = 3,5 / 4 = 0,875

Die Tangentensteigung an der Stelle x=3 ist m_T = f '(3) = -1

Schnittwinkel:  tan(α) = | (m_G - m_T) / ( 1 + m_G • m_T) | = 15  →  α ≈ 86,2°

b)

Die Gerade durch den Punkt P( x_p | y_p ) mit der Steigung m hat die Gleichung

y = m • ( x - x_p ) + y_p            [ Punkt-Steigungs-Formel ]   

Ist x=b die (noch nicht bekannte) Berührstelle, also B(b|f(b)) der Berührpunkt dann gilt:

Tangente:    y = f '(b) • ( x  - b ) + f(b)   = (- b + 2) • (x - b)  - 1/2 b² + 2b + 2

Einsetzen von P(-1 | 0):

0 = (-b + 2) • (-1- b)  - 1/2 b² + 2b + 2

Ausmultiplizieren und zusammenfassen:

0 = b • (b+2) / 2  →  b = 0 oder b = -2   [ Editiert gemäß Kommentar von Georgborn]

Tangente:  y = f '(b) • (x - b)  + f(b)

y = 2x + 2  in B₁(0|2)   und  y= 4x+4  in B₂(-2|-4)

Gruß Wolfgang

Comments

Hallo Wolfgang,

Der Vollständigkeit halber :
In den Frageformulierungen ist zwar nur von 1Tangente die Rede, aber
Hinweis : es gibt 2 Tangenten für b.)
siehe meine Antwort

mfg Georg

---

Hallo Georg,

du hast recht, danke für den Hinweis. Habe es mit Hinweis auf deinen Kommentar editiert.

Habe den Term wohl falsch in meinen Rechner eingetippt.

Gruß Wolfgang

---

Hallo Wolfgang,

Welche gerade durch den Punkt P(-1/0) ist tangente an den Graphen von f

In der Fragestellung ist ja nur von 1 Tangente die Rede.

Zu deiner  Information :
Mein Matheprogramm, welche ich aus Arbeitsersparnissgründen manchmal
nutze, zeigte mir als Ergebnis 2 Stellen an.
Zuerst dachte ich an einen Fehler.
Dann zeigte es sich das dies richtig war.

Allgemeinplatz. Binsenweisheit.
Keiner ist perfekt.
Das hat noch niemand geschafft.

Hier zu deiner Information noch meine soeben verfasste e-mail
an den Forumsbetreiber. Wenn du magst kannst du dich auch dazu
äußern.

In den letzten Tagen bin ich von " Gast " hier im Forum mehrmals gemobbt worden.

https://www.mathelounge.de/331396/mathematik-ratsel-vergessen-erwahnen-altester-sohn-einen
" Du vergisst häufig. "

Es geht noch nicht einmal mehr darum mich auf eventuelle Fehler in meinen Rechnungen
aufmerksam zu machen. Es sind Angriffe auf meine Person.

Leider kann ich mich persönlich nicht wehren. Dazu fehlt mir das Gegenüber.

Es wird für mich unerträglich.
Ich verstehe nicht wieso im Forum diesen Leuten eine Plattform dafür gegeben wird..

MIt Mathematik hat dies nichts mehr zu tun. Diese Leute vergiften hier nur die Atmossphäre.

Ich halte meinen Vorschlag, verdienstvolle Mitarbeiter sollten Forumsnutzer sprerren
lassen können,  für sinnvoll.

Dann wäre dem Spuk ein Ende gesetzt.

Probeweise werde ich mich für nächste Woche hier aus dem Forum verabschieden.

Answer 2

Hier eine Skizze für den Sachverhalt ( symbolisch )

P1 ( -1 | 0 )
f ( x ) = -1/2x²+2x+2
f ´( x ) = - x + 2

-x + 2 = [ ( -1/2 * x^2 + 2 x + 2 ) + 0 ] / [  x - ( -1 ) ]

Es gibt 2 Lösungen / Stellen
x = 0
und
x = -2

1.)
x = 0
f ´( 0 ) = -0 + 2 = 2

Tangentengleichung
y = m * x + b
0 = 2 * (-1) + b
b = 2
y = 2 * x + 2

2.)
x = -2
f ´( -2) = - ( -2 ) + 4 = 4

Tangentengleichung
y = m * x + b
0 = 4 * (-1) + b
b = 4
y = 4 * x + 4

~plot~ -1/2 * x^2 + 2 x + 2 ; 2 * x + 2 ; 4 * x + 4 ~plot~