Kostenfunktion quadratisch

Question

Ein Betrieb hat monatliche Fixkosten von € 5000. Bei einer Produktion von 100 Stück fallen Kosten in der Höhe von € 6300 an, bei einer Produktion von 200 Stück betragen die Kosten € 8100. 

a) Stellen Sie die Gleichung der quadratischen Kostenfunktion auf.

b) Ermittle, wie viel Stück maximal produziert werden dürfen, wenn die Kosten eine Höhe von € 10 000 nicht überschreiten dürfen. (Wie komme ich auf a,b und c? Wie berechnen ich die unbekannten?)
c) Stelle eine neue Kostenfunktion für den Betrieb auf, wenn sich die Fixkosten auf 80 % reduzieren und die variablen Kosten um 20 % steigen. 
Dankeee :)

Answer 1

a)

Ansatz:  K(x) = ax² + bx + 5000

K(100) = 6300  und  K(200) = 8100    →   a,b aus 2 Gleichungen mit 2 Unbekannten

[ Kontrollergebnis: a = 1/40 und  b = 21/2 ]

b)

K(x) ≤ 10000  ⇔ K(x) - 10000 ≤ 0

K(x) - 10000    eine nach oben geöffnete Parabel mit den Nullstellen x₁ und x₂, x₁ ist negativ.

Die Kosten sind also ≤ 10000 für  x ∈ [ 0 ; x₂ ]

Hier kannst du deine Ergebnisse ungefähr überprüfen:

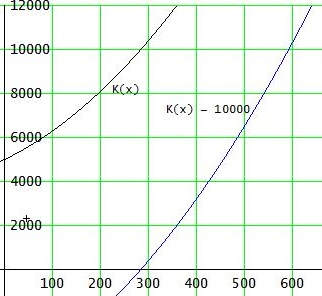
Gruß Wolfgang

Comments

K(x) = 0,025·x² + 10,5·x + 5000

c) Stelle eine neue Kostenfunktion für den Betrieb auf, wenn sich die Fixkosten auf 80 % reduzieren und die variablen Kosten um 20 % steigen.  

Kneu(x) = (0,025·x² + 10,5·x)*(1 + 0.2) + (5000)*0.8 = 0.03·x^2 + 12.6·x + 4000

---

Das Problem bei mir ich komm nicht auf die Zahlen beim Gleichungssytem bei mir kommt immer wieder eine negative Zahl oder die falsche Zahl...

---

a·100² + b·100 + 5000 = 6300  und  a·200² + b·200 + 5000 = 8100

vereinfachen

wenn du dann die 1. Gleichung mit 2 multiplizierst und das Ergebnis von der zweiten subtrahierst, fällt b heraus und du kannst nach a auflösen.