jetzt haben schon vier Leute geantwortet und nur einer hat's gemerkt. Die oben angegebene Funktion ist weder quadratisch noch linear, sondern beides! Die Werte mit \(x\le 1,2\) werden recht genau durch die Parabel \(p(x)= 32,202x^2+3,21\) abgedeckt und die Werte \(x \ge 1,2\) erfüllen die lineare Funktion \(g(x)=77,35x-43,20\).
Auf diesem Bild ist es gut zu sehen:
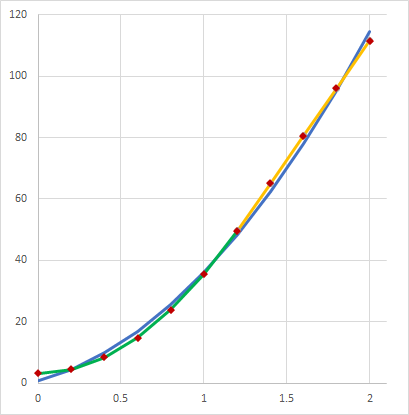
Die roten Rauten sind die Messwerte. Die blaue Kurve ist die Parabel für alle Punkte mit dem 'best fit'. Sie tifft die Punkte ungefähr. Die grüne Parabel und die gelbe Gerade sind die Graphen der Funktionen \(p(x)\) und \(g(x)\) (s.o.).
Und wie kann man das feststellen? Man macht sich zunutze, dass die x-Werte äquidistant sind - d.h. das Delta zweier auf einander folgender x-Werte ist immer konstant (hier \(\Delta x=0,2\)). Dann stellt man sich eine Tabelle auf, und berechnet die Differenzen der y-Werte und die Differenzen der Differenzen:$$\begin{array}{rr|rr}x& y& \Delta y& \Delta^2 y\\ \hline 0& 3,2& & \\ 0,2& 4,5& 1,3& \\ 0,4& 8,4& 3,9& 2,6\\ 0,6& 14,8& 6,4& 2,5\\ 0,8& 23,8& 9& 2,6\\ 1& 35,4& 11,6& 2,6\\ 1,2& 49,6& 14,2& 2,6\\ 1,4& 65,1& 15,5& 1,3\\ 1,6& 80,6& 15,5& 0\\ 1,8& 96& 15,4& -0,1\\ 2& 111,5& 15,5& 0,1\end{array}$$Sind die Werte \(\Delta y\) konstant, so handelt es sich um eine Gerade und sind die Werte in der Spalte \(\Delta^2 y\) konstant und verschieden von 0, so folgt dieses Stück einer Parabel.