> Wie kann man ausrechnen wo der Abstand zwischen den zwei Funktionen am geringsten ist?
"Wo" klingt eigentlich mehr nach einer gesuchten Stelle x, (Aber deren aufwändige Berechnung und die Wahl der beiden Funktionen legen Mathecoachs Interpretation der nach meiner Meinung unklaren Frage nahe)
f(x) = ex , g(x) = ln(x)
Abstand beider Funktionenan an einer Stelle x:
d(x) = | ex - ln(x) | = ex - ln(x) (wegen ex > ln(x) für alle x.
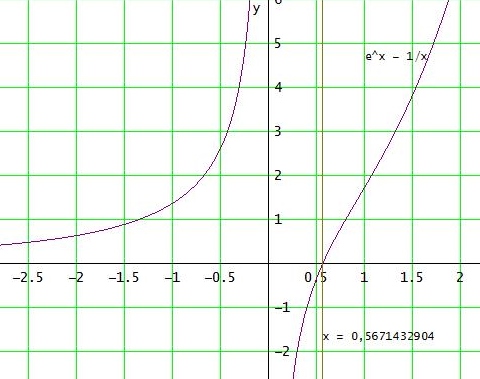
d'(x) = ex - 1/x = 0 mit VZW von - → + ergibt die Minimalstelle.
diese Gleichung kann wohl nicht explizit nach x auflösen:
Man benutzt ein numerisches Näherungsverfahren, zum Beispiel das
Newtonverfahren:
die unten genannte Funktion f ist hier d' (f ' = d'')
gesucht sind die Nullstellen von f(x) = ex - 1/x:
Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man immer bessere Werte mit der Formel
xneu = xalt - f(xalt) / f ' (xalt)
Infos dazu findest du hier:
https://de.wikipedia.org/wiki/Newton-Verfahren
[ Rechnerlösung: x = 0,5671432904 ]
Gruß Wolfgang