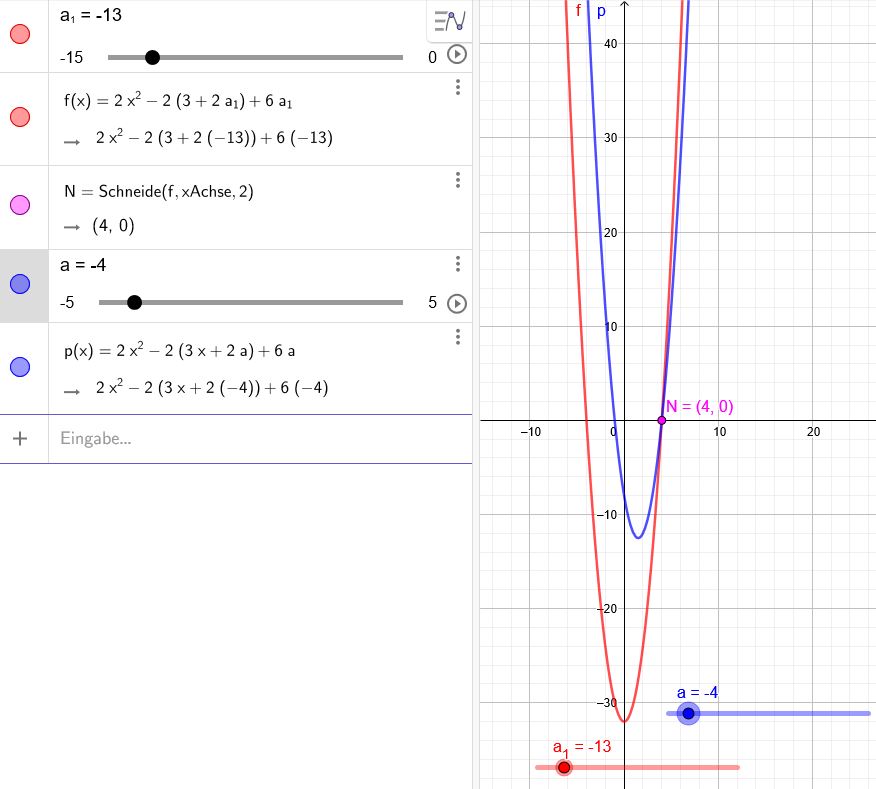
Wählen Sie ein geeignetes a so, dass 4 eine Nullstelle der Funktion mit \(\red {f(x)=2x^2-2(3+2a)+6a}\) ist
\(2x^2-2(3+2a)+6a=0\)
\(2x^2-6+2a=0\)
\(x^2=3-a\)
\(x_1= \sqrt{3-a} \)
Nun soll 4 eine Nullstelle sein:
\(4= \sqrt{3-a}|^{2} \)
\(16= 3-a \)
\(a=-13\)
\(x_2= -\sqrt{3-a} \)
\(4= -\sqrt{3-a} \)
\(-4= \sqrt{3-a}|^{2} \)
Ergibt auch wieder \(a=-13\)
Version mit eventuell fehlendem \(x\) (Kommentar von Lu)
\(\blue {p(x)=2x^2-2(3x+2a)+6a}\)
\(2x^2-2(3x+2a)+6a=0\)
\(x^2-3x+a=0\)
\(x^2-3x=-a\) Quadratische Ergänzung :
\(x^2-3x+2,25=-a+2,25\) 2. Binom:
\((x-1,5)^2=-a+2,25|±\sqrt{~~} \)
1.)
\(x-1,5=\sqrt{2,25-a} \)
\(x_1=1,5+\sqrt{2,25-a} \) Nun soll 4 eine Nullstelle sein:
\(4=1,5+\sqrt{2,25-a} \)
\(2,5=\sqrt{2,25-a} |^{2} \)
\(6,25=2,25-a\)
\(a=-4\)
2.)
\(x-1,5=-\sqrt{2,25-a} \)
\(x_2=1,5-\sqrt{2,25-a} \) Nun soll 4 eine Nullstelle sein:
\(4=1,5-\sqrt{2,25-a} \)
\(2,5=-\sqrt{2,25-a} \)
\(-2,5=\sqrt{2,25-a} |^{2} \)
Auch wieder \(a=-4\)