allgemeine Lösung der eulerschen DGL ermitteln

Question

Gegeben ist die DGL

x² y'' - 3xy' + 7y = 0   x>0

Sie soll mit  x = e^t substituiert werden um eine DGL mit konstanten Koeffizienten für y in Abhängigkeit von t zu erhalten. Wie genau gehe ich da vor?

Answer 1

x² y'' - 3xy' + 7y = 0   x>0

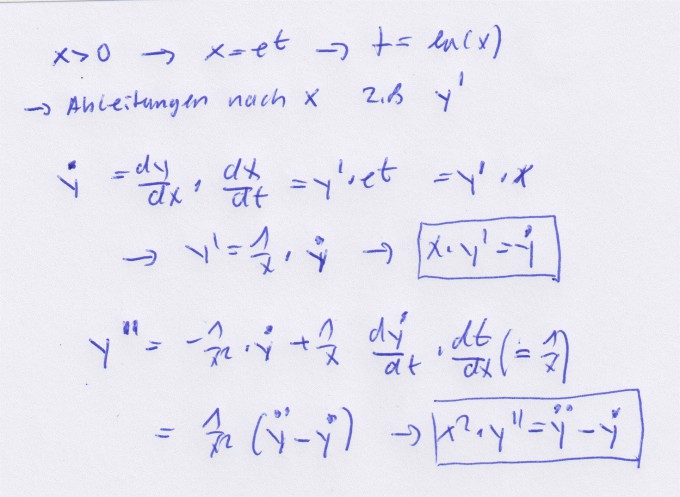
daraus folgt:

x^2 y''= y'' -y'
x*y'= y'

eingesetzt:

y'' -y' -3y' +7y=0
y'' -4y' +7y    =0

--------<charakt. Gleichung:
k^2 -4k +7=0

k_1.2=  2± i√ 3

y(t)= C_1 x^{2 +i√3} +C_2 x^{2 -i√3}

Rücktransformation rechnerisch oder aus der Tabelle:

Lösung:

y= C_1 x^2 *cos(√3 *ln(x)) +C_2 x^2 *sin(√3 *ln(x))