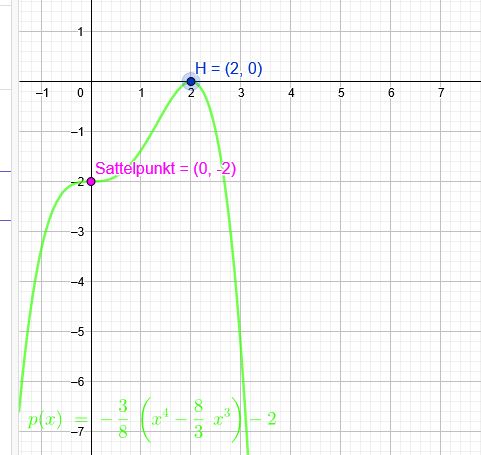
Eine Parabel der 4. Ordnung hat in H \((2|0)\) einen Hochpunkt und in P\((0|-2)\) einen Sattelpunkt. Bestimme die Gleichung der Parabel.
P\((0|-2)\) ↑ P'\((0|0)\) Dreifachnullstelle:
\(f(x)=ax^3(x-N)=a(x^4-Nx^3)\)
\(f'(x)=a(4x^3-3Nx^2)\)
H\((2|...)\) waagerechte Tangente:
\(f'(2)=a(32-12N)=0\)
\(N=\frac{8}{3}\):
\(f(x)=a(x^4-\frac{8}{3}x^3)\)
H \((2|0)\) ↑ H´\((2|2)\):
\(f(2)=a(16-\frac{64}{3})=-\frac{16}{3}a=2\)
\(a=-\frac{3}{8}\):
\(f(x)=-\frac{3}{8}(x^4-\frac{8}{3}x^3)\) ↓
\(p(x)=-\frac{3}{8}(x^4-\frac{8}{3}x^3)-2\)