Rotation um y-Achse von f(x) = (a-x)1/3

Question

die Kurve f(x)=(a-x)^{1/3} soll um die y-Achse rotieren.
Zuerst bilde ich die Umkehrfunktion.
Wie ermittle ich dann die Grenzen?

Comments

das soll heißen 3. Wurzel aus (a-x), etwas unleserlich dargestellt

Answer 1

Das hier ist y = (5-x)^1/3 
Die Grenzen sind y=0 und y = 5^1/3 ≈ 1.70998
Du brauchst deshalb 0 und a^1/3 als Grenzen.

Die Umkehrfunktion kannst du selbst ermitteln. (oder?)

Comments

Die Umkehrfunktion kann ich ermitteln.
Warum nimmt man von (5-x)^{1/3} die 5, weil das eine Nullstelle ergeben würde, wenn man die einsetzt?

---

Auf der y-Achse ist x=0.

y = (a-0)^{1/3} = a^{1/3}

Answer 2

y = (a - x)^1/3

Umkehrfunktion bilden:

a - x = y³
x = a - y³
y = a - x³

Für die Grenzen überleg dir mal, wie diese Funktion aussieht. Überleg dir auch in welchen Grenzen die Originalfunktion definiert ist.

Die Grenzen sollten sicher von 0 bis nur Nullstelle sein. 

y = a - x³ = 0
x = a^1/3

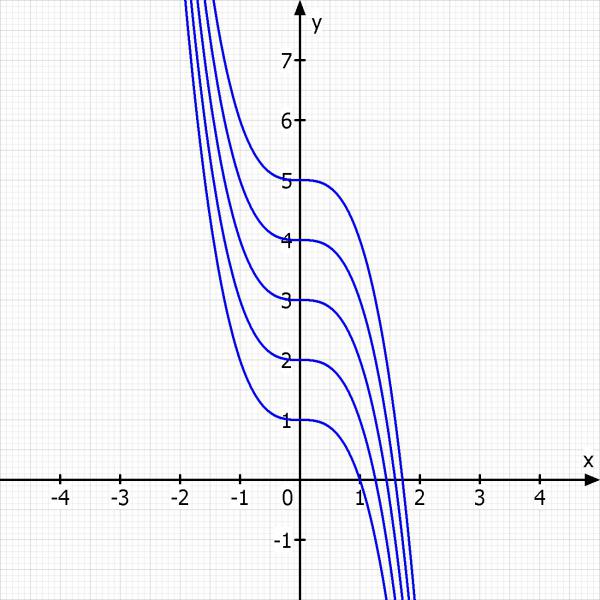
Ich skizziere mal die Umkehrfunktion.