steckbriefaufgabe,achsenschittpunkt,2 kurven

Question

kann diese Aufgabe nicht lösen :(

 Eine Parabel 3.Ordnung hat die selben Achsenschnittpunkte wie y=2x.1/2x^3. Beide Kurven stehen in O(0/0) senkrecht aufeinander.

Comments

korrektur* y=2x-1/2x^3

---

Ist immer noch nicht eindeutig

  - y = 2 * x - ( 1/2) * x³

  - y = 2 * x - 1/ ( 2 * x^3 )

  mfg Georg   

Answer 1

Nullstellen bestimmen

0=2x- 1/2 x³   

0=x(2- 1/2 x²)                        x₁= 0

0= 2-1/2 x²                             x_2,3 = ±2

Damit die gesuchte Kurve senkrecht auf der  angegebenen Kurve steht , die Vorzeichen ändern.

f( x)= -2x +1/2 x³

 Um es  überprüfen zu können , entweder zwei Wertetabellen anlegen und/ oder die beiden Kurven zeichnen.

Comments

Hallo Akelei,

  es dürfte ein Fehler vorhanden sein. Bei zwei senkrecht aufeinander
stehende Geraden ist der Zusammenhang der Steigung ( t für tangente,
n für normale ) n = 1 / -t gegeben.

[ 2 * x  - 1/2 * x^3  ]´ = 2 - 1/2 * x^2 für x = 0 : t  = 2
[ -2 * x  + 1/2 * x^3  ]´ = -2 + 1/2 * x^2 für x = 0 : n = -2

Sollte aber heißen n = 1/ -2 = - 1/2
( siehe meine hoffentlich fehlerfreie Antwort )

mfg Georg

Answer 2

Schnittpunkte mit der x-Achse

( 0,0 ) ( -2,0 ) ( 2,0)

Steigung für [ 2 * x  - 1/2 * x³  ]´ = 2 - 1/2 * x² für x = 0 : m  = 2

Steigung für die zu suchende Funktion bei x = 0 : mf = - 1/2

f(x) = a*x^3 + b*x^2 + c*x + d
f(0) = 0 -> d = 0
f(2) = a*2^3 + b*2^2 + c*2 = 0
8*a + 4*b + 2*c =0
f(-2) = a*(-2)^3 + b*(-2)^2 + c*(-2)
-8*a + 4*b -2*c = 0
f´(x) = 3*a*x^2 + 2*b + c
f´(0) = c = -1/2

b = 0
a = 1/8

f(x) = 1/8 * x^3 - 1/2 * x

mfg Georg

Bei Fehlern oder Fragen wieder melden

 

Answer 3

f(x) = 2x - 1/2*x^3

Akelei hat die Nullstellen mit -2, 0, 2 richtig bestimmt.

Damit lautet die Gesuchte Funktion in der Nullstellenform.

g(x) = a·x·(x + 2)·(x - 2) = a·x·(x^2 - 4) = a·x^3 - 4·a·x

Nun sollen die Steigungen im Koordinatenursprung senkrecht zueinander sein.

Steigung von f(x) im Koordinatenursprung

f'(0) = 2 - 3/2*0^2 = 2

D.h. die Steigung unserer Funktion muss -1/2 sein.

g'(0) = 3·a·0^2 - 4·a = -1/2
- 4·a = -1/2
a = 1/8

D.h. unsere Funktion lautet

g(x) = 1/8·x·(x + 2)·(x - 2)

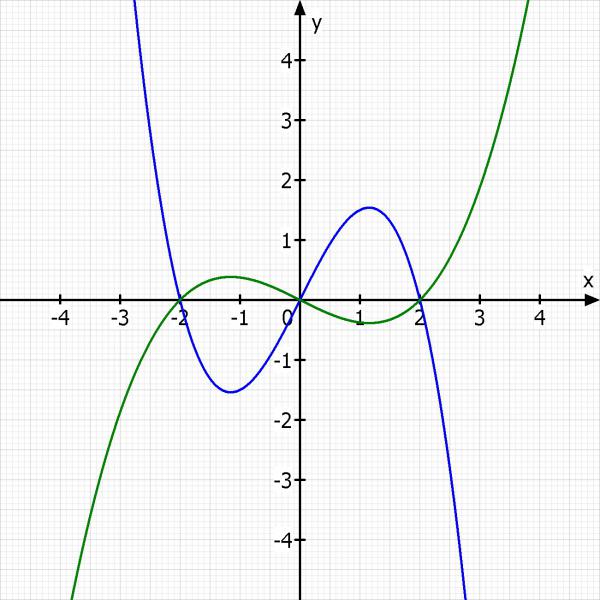
Ich zeichne die Funktionen mal damit du dir das besser vorstellen kannst.