die angehängte Aufgabe muss ich lösen, aber leider bekomme ich es einfach nicht hin. Wäre jemand so nett und würde mir dabei helfen?
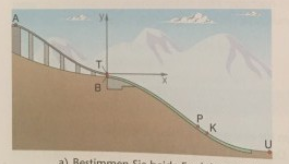
Aufgrund des unten abgebildeten Profils einer Skischanze wird deutlich, dass sowohl der Anlauf als auch die Aufsprunghügel durch jeweils eine Funktion beschrieben werden können. Hierbei soll der Ursprung des Koordinatensystems am Ende des Schanzentisches T liegen.
Die genauen Daten:
Der Anlauf beginnt im Punkt \( A(-110| 48,79) \) und der Schanzentisch hat den Steigungswinkel \( -11°\)
Aufsprunghügel:
Hangbeginn \( \mathrm{B}(\mathrm{O} |-3,14) \)
Aufsprungunkt \( z.B. \text { } \mathrm{P}(95,4|-53,56) \)
Kalkulationspunkt \( \mathrm{K}(107,9|-62,6) \)
Ende des Hanges U \( (178,7|-86) \)
Alle Koordinatenangaben in Meter
a) Bestimmen Sie beide Funktionsgleichungen.
b) Wie steht es mit der Sicherheit?
Die Funktionsgleichung \( \mathrm{f}_{1}(\mathrm{x})=-0,006 \cdot \mathrm{x}^{2}+\mathrm{t} \cdot \mathrm{x} \) beschreibt näherungsweise die Flugbahn eines Skispringers.
Für welche t endet der Sprung vor bzw. hinter dem Kalkulationspunkt?
c) Die Sprünge beeindrucken immer wieder auch durch die Höhe des Fluges über dem Aufsprunghügel. Welche maximale Hóhe erreicht ein Springer nach der oben gegebenen Modellgleichung, wenn er genau im Kalkulationspunkt landet? Wie wirkt es sich aut die maximale Höhe aus, wenn der Sprung 5 m über den K-Punkt hinausführt?