Also wenn du die Querschnittsform der Sprungschanze von der Seite durch eine Polynomfunktion 3. Grades modellieren willst, kann man sich folgende Skizze überlegen:
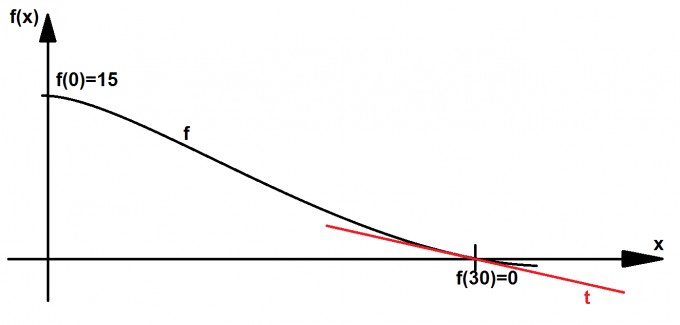
Dann kann man auch daraus vier Bedingungen ablesen:
Ansatz:
$$ f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c $$
$$ \begin{aligned}&(1) &f(0)&=15\Rightarrow d=15\\&(2) &f'(0)&=0\Rightarrow c=0\\&(3) &f(30)&=0\\&(4) &f'(30)&=-\frac{1}{4} \end{aligned} $$
Dann hat man nur noch ein LGS mit zwei Gleichungen und zwei Unbekannten zu lösen:
$$ \begin{aligned}&(3) &27000a+900b&=-15\\&(4)&2700a+60b&=-\frac{1}{4} \end{aligned} $$
Als Lösung hat man dann $$ a=\frac{1}{1200}\\b=-\frac{1}{24} $$, also
$$ f(x)=\frac{1}{1200}x^3-\frac{1}{24}x^2+15 $$
Tangentengleichung an der Sprungschanze würde so aussehen:
$$ t(x)=mx+n \text{ mit } (3),(4) \text{ ergibt dann }\\ 0=-\frac{1}{4}\cdot 30+n\Rightarrow n=\frac{15}{2}$$also
$$ t(x)=-\frac{1}{4}x+\frac{15}{2} $$