Minimaler Abstand zwischen Funktion und Umkehrfunktion

Question

Gegeben ist die Funktion: y = x^2 +1

Skizzieren Sie die Funktion und die zugehörige Umkehrfunktion. Berechnen Sie den minimalen Abstand zwischen der Funktion und der Umkehrfunktion.

Ansatz:

Umkehrfunktion: y = √(x-1)

Jetzt wollte ich mittels Lagrange ein Gleichungssystem aufstellen, jedoch weiß ich nicht genau wie. Kann mir jemand weiterhelfen?

Answer 1

Meine Überlegungen

es gibt bei diesen Fragen die Möglichkeiten : was ist mit min Abstand gemeint.

Ist es

-  der senkrechte Abstand ( Differenzfunktion )

oder

- der Abstand senkrecht über die Winkelhalbierende

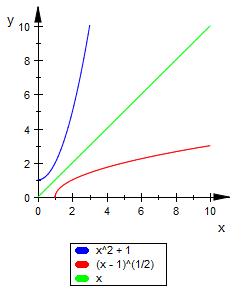
Ich denke der zweite Fall ist gemeint

Frage : wie ermittele ich den kürzesten Abstand der Winkelhalbierenden
zur Ausgangsfunktion. Indem ich die Winkelhalbierenden als Tangente an die
Funktion schiebe.
f ´( x ) = 2 * x
1 ist die Steigung der Winkelhalbierenden
2 * x = 1
x = 0.5
( 0.5 | 1.25 )

Wird dieser Punkt  an der Winkelhalbierenden gespiegelt ergibt sich
auf der Umkehrfunktion der Punkt

( 1.25 | 0.5 )

Nun noch den Abstand der beiden Punkte über den
Pythagoras berechnen.

Comments

Δ x = ( 0.5 - 1.25 ) = - 0.75
Δ y = ( 1.25 - 0.5 ) = 0.75

Abstand ^2 = ( Δ x )^2 + ( Δ y )^2
Abstand = 1.061

( Δ x )^2  ist immer  ( Δ y )^2
Können wird uns die Berechnung von Δ y  auch noch sparen

Abstand ^2 = 2 * ( Δ x )^2

Answer 2

Die Graphen von Funktion und Umkehrfunktion sind Urbild und Bild bei Spiegelung an der Geraden mit der Gleichung y = x. Der Abstand zwischen den Graphen wird senkrecht dazu gemessen, also entlang einer Geraden mit der Gleichung y = b - x. Welches b da zu wählen ist, das ist genau die Frage der Aufgabe. Der Schnittpunkt S zwischen den Geraden mit den Gleichungen y = x und y = b - x ist S(b/2; b/2). Der Schnittpunkt  zwischen den Graphen mit den Gleichungen y = b - x und y = x² +1 sei R. Dann gibt es ein b, für welches der Abstand der Punkte R und S voneinander am kleinsten wird. Für dieses b ist auch der Abstand der Graphen von Funktion und Umkehrfunktion am kleinsten.

Comments

Hallo Roland,
was bekommst du heraus ?

---

Ich bekomme b = 7/4 heraus. Aber dein Lösungsweg ist viel besser. Übrigens mit dem gleichen Ergebnis.