Hallo
Stimmt die folgende Lösung und der folgende Lösusngsweg(Lineare Optimierung)?
Aufgabe: Ein Baugeschäft liefert 1000 Säcke Kalk an drei Baustellen B1, B2, B3. Der Kalk wird in zwei Lagerhallen L1 und L2 an verschiedenen Orten gelagert. Die Transportkosten rpo Sack, der Bedarf an Kalk pro Baustelle und dei Lagerbestände sind in nachfolgender Tabellersichtlich. Wie muss der Transport organisiert werden, damit die gesamten Transportkosten minimal sind? Wie viel betragen sie? Folgend eine Überischtstabelle:
Transportkosten pro Sack in €
L1 L2 |
| |
B1
| 0.9 0.6 | 300 |
|
| B2 | 1 0.4 | 500 |
|
B3
| 1.2 1 | 200 |
|
| Lagerbestände(in Säcken) | 600 400 | 1000 |
|
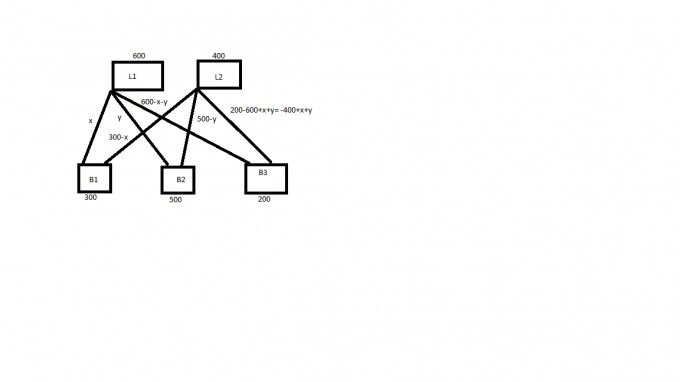
(Tabelle verschoben, zu "Bedraf an den Baustellen" gehört die Spalte mit den Zahlen 300,500, 200, 1000 und die Spalte 0.9,1,1.2 gehört zu den Transportkosten von Lagerhalle 1 zu den jeweiligen Baustellen B1, B2, B3 und dei Spalte 0.6,0.4,1 zu den Transportkosten von Lagerhalle 2 aus zu den jeweiligen Baustellen B1, B2, B3)
Mein Lösungsweg:
1. x>=02. y>=03. 300-x>=0 somit x<=3004. 500-y>=0 somit y<=5005. 600-x-y>=0 somit y<=-x + 6006.-400+y+y>=0 somit y>= -y + 400
7. Zielfunktion: 0.9*x+0.6*(300-x) + < + 0.4*(300-y) + 1.2*(600-x-y) -400+x+y somit Z= 0.1x+490+2.88y (Z= Zielfunktion) somit y= -1/28x -175 +14/5Z
(Die Funktionen 1-6) ergeben sich ausgehend aus der gewählten Beschriftung in der angehängten Grafik)
Meine Lösung: Es müssen von L1 aus nach B1 0 Säcke, nach B2 500 Säcke, nach B3 100 Säcke und von L2 nach B1 300 Säcke, nach B2 0 Säcke und nach B3 100 Säcke transportiert werden. die Transportkkosten betragen Z= 0.1*0 + 490 +2.8*500 = 14490€Danke