Lagrange Verfahren
f(x, y, k) = x·(y - 1) + k·(x^2 + y^2 - 1)
df / dx = 2·k·x + y - 1 = 0
df / dy = x + 2·k·y = 0
df / dk = x^2 + y^2 - 1 = 0
Das Gleichungssystem liefert die Lösung: x = - √3/2 ∧ y = - 1/2
x·(y - 1) = (- √3/2)·((- 1/2) - 1) = 3·√3/4
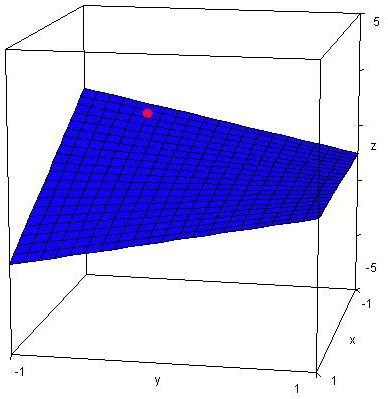
Skizze