Wie bildet man die Ableitung bei dieser Betragsfunktion?

Question

Wie bilde ich bei folgender Betragsfunktion die Ableitung:

f(x)= Ix ^2 − 1 I

Answer 1

Die Funktion ist an den Stellen \(x=-1\) und \(x=1\) nicht differenzierbar, sonst schon. Löse den Betrag auf und leite intervallweise ab.

Answer 2

die Ableitung des Betrags lautet :

$$  \frac { d }{ dx }(\vert x \vert)=\frac { x }{ \vert x \vert } $$ für x≠0

Mit der Kettenregel folgt:

$$  \frac { d }{ dx }(\vert (x^2-1) \vert)=\frac { (x^2-1)*2x }{ \vert (x^2-1) \vert } $$

für x≠±1

Answer 3

f(x) =  (  x² - 1         für  x ∈ ] - ∞ ; -1 ] ∪ [ 1 ; ∞ [

           ( - (x² - 1)     für  x ∈ ] -1 ; 1 [

Für x ≠ ±1 gilt für die Ableitung der eingeschränkten Funktion f_e :

f_e '(x)  =_ℝ\{±1}  (   2   für  x ∈ ] - ∞ ; -1 [ ∪ ] 1 ; ∞ [

                           (  -2   für  x ∈ ] -1 ; 1 [

wegen lim_{x→ 1+}    f_e^'(x)  = 2   ≠  -2  = l im_x→1-  f_e'(x) ist f nicht diffbar in x = 1

wegen lim_{x→ -1+}   f_e'(x)  = -2  ≠   2  =  lim_x→1-  f_e'(x) ist f nicht diffbar in x = -1

-----------

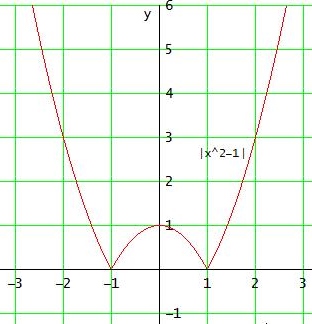
Anschaulich ist f in x = ± 1 nicht differenzierbar, weil der Graph dort jeweils einen "Knick" hat, so dass keine eindeutige Tangentensteigung definiert werden kann.

Gruß Wolfgang