Bestätigung, dass sich Tangenten an einer bestimmten Stelle schneiden

Question

Ich brauche eure Hilfe,und zwar:Es sei f(x)=2/x + 2.   Bestätige durch Rechnungen, dass sie die Tangenten an der Stelle x=1 und x=-3 auf der x-Achse schneiden! Danke

Answer 1

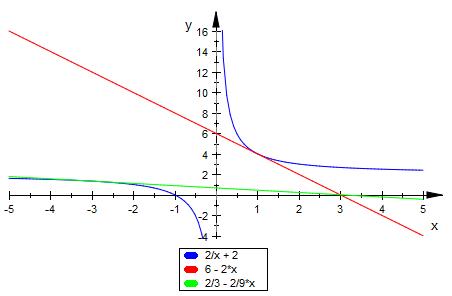
Ich brauche eure Hilfe,und zwar:Es sei f(x)=2/x + 2.   Bestätige
durch Rechnungen, dass sie die Tangenten an der Stelle
x=1 und x=-3 auf der x-Achse schneiden! Danke

f ( x ) = 2 / x + 2
f ´ ( x ) = -2 / x²

Die beiden Tangentengleichungen aufstellen.

Tangente allgemein
f  ( x ) = t ( x )
f ´( x ) = t ´( x )

1.Tangente
f ( 1 ) = 2/1 + 2 = 4
f ´( 1 ) = -2

y = m * x + b
4 = -2 * 1 + b
b = 6

1.Tangente
t1 ( x ) = -2 * x + 6
Schnittpunkt mit der x-Achse : y = 0
0  = -2 * x + 6
x = 3

2.Tangente
f ( -3 ) = 2/(-3) + 2 = 4/3
f ´( -3 ) = -2/(-3)² = -2 /9

y = m * x + b
4/3 = -2/9 * (-3) + b
b =  2/ 3

2.Tangente
t2 ( x ) = -2 / 9 * x + 2/3

Schnittpunkt mit der x-Achse : y = 0
0 = -2 / 9 * x + 2 / 3
2 / 9 * x = 2 / 3
x = 18 / 6
x = 3

Beide angenten haben den gleichen Schnittpunkt mit der x = Achse
bei x = 3

 

Comments

Ich bin gerade total verwirrt!Und zwar habe ich bei f´(x) = -(2/1)² = 4 raus und nicht -2 :(!Und wie kommen sie bei der Ableitung auf -2/x² ??Liebe Grüße von Sonnenschein1

---

f ( x ) = 2 / x + 2

f ( x ) = 2 * x^-1 + 2
Potenzregel
f ´( x ) = 2 * ( -1 ) * x ^-1-1
f ´( x ) = - 2 *  x ^-2
f ´( x ) = - 2 *  / x ²

noch deutlicher
f ´( x ) = - 2 *  / ( x ² )
Vergleiche mit deiner Ableitung.

Answer 2

f ' (x) = -2 / x² also f ' (1) = - 2 und f ' (-3 ) = - 2 / 9

t1:   y = mx + n    m= -2   P ( 1 / 4 )

       4 = -2 * 1 + n  gibt n = 6 .

t1 :   y = -2x + 6

t2:     y = mx + n    m= -2 /9    P ( -3 /   (4/3)   )

4/3 =  -2 / 9 * -3  + n   gibt  n = 2/3

t2:   y = -2/9  * x +  2/3 

Schnitt     -2x + 6   =  -2/9  * x +  2/3 

x = 3   y =  0    Passt, liegt auf der x-Achse

Comments

Ich bin gerade total verwirrt!Und zwar habe ich bei f´(x) = -(2/1)² = 4 raus und nicht -2 :(!Und wie kommen sie bei der Ableitung auf -2/x² ??Liebe Grüße von Sonnenschein1 

Answer 3

f(x) = 2/x + 2

f'(x) = - 2/x²

t1 = f'(1) * (x - 1) + f(1) = 6 - 2·x

t2 = f'(-3) * (x + 3) + f(-3) = 2/9·(3 - x)

Beide Tangenten schneiden die x-Achse bei 3 wie man leicht sehen kann.

Comments

Ich bin gerade total verwirrt!Und zwar habe ich bei f´(x) = -(2/1)² = 4 raus und nicht -2 :(!Und wie kommen sie bei der Ableitung auf -2/x² ??Liebe Grüße von Sonnenschein1 

Answer 4

Hallo Sonnenschein,

f((x) = 2/x +2     f(1) = 4   → B₁ = (1|4)   ,   f(-3) = 4/3 → B₂ = (-3 | 4/3)

f '(x) =  -2/x²      f '(1) = -2  →  m₁ = -2   , f '(4/3) = -2/9

Die Gerade durch den Punkt P( x_p | y_p ) mit der Steigung m hat die Gleichung

y = m • ( x - x_p ) + y_p            [ Punkt-Steigungs-Formel ]   

Tangente 1:   y = -2 • (x - 1) + 4   = -2x + 6

Tangente 2:  y =  - 2/9 • (x  + 3) + 4/3  = -2/9 x +2/3

Tangentenschnittpunkt S:

-2x+6 = -2/9 x +2/3  → x =3  

f(3) = 0  → Schnittpunkt der Tangenten auf der x-Achse in S(3|0)

Gruß Wolfgang

Comments

Ich bin gerade total verwirrt!Und zwar habe ich bei f´(x) = -(2/1)² = 4 raus und nicht -2 :(!Und wie kommen sie bei der Ableitung auf -2/x² ??Liebe Grüße von Sonnenschein1

---

> wie kommen sie bei der Ableitung auf -2/x² 

[ 2/x ] ' = [ 2 * x^-1] ' = 2 * (-1) * x^-2  = -2 / x²

^> habe ich bei f´(x) = -(2/1)² = 4 raus und nicht -2

- (2/1)² = -4

(-2/1)² = 4

---

und wie komme sie bei f´(1)= auf -2 ? Ich komme da auf 4

---

f '(1) = -2 / 1² = -2   ( und wir sind hier (fast) alle per Du :-))

---

ahh dankeich habe es als bruch in meinen Taschenrechner eingegeben, deshalb kam was anderes raus! Danke für die schnellen Antworten