Kurvendiskussion & Textaufgabe

Question

Ich komme leider nicht weiter, kann mir jemand helfen bzw. mir es vorrechnen?

Comments

Könnt ihr mir diese Aufgabe vorrechnen ? Ich komme nicht weiter bitte :/

---

Die Parabel ist bei mir nicht zu sehen.

mfg Georg

---

Die Parabel ist bei mir nicht zu sehen.

Du kannst sie dir etwas weiter unten im Beitrag von Wolfgang ansehen.

Dort findest du auch die Lösung der Aufgabe.

Answer 1

Du musst 

1) die lage der Parabel im KS festlegen, weil deren Gleichung gebraucht wird

2) Zielfunktion A(x) bestimmen                  weil diese maximal werden soll

3) Ableitungen A' und A" bestimmen        weil man damit das Maximum findet

4) A'(x) = 0 lösen                                          weil das die möglichen Extremwerte ergibt

5) Lösungen in A"(x) einsetzen                 weil A"(Lösung) < 0  → Maximum

6) f(Lösung)  bestimmen                             weil Breite und Höhe der Tür gesucht sind

----------------------

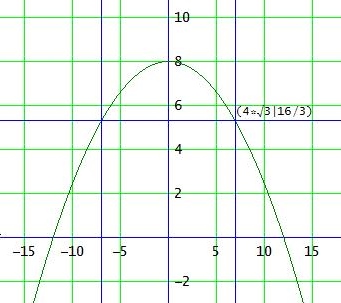
Lege also die Parabel ins Koordinatensystem mit dem Scheitelpunkt S(0|8)

Sie hat dann die Nullstellen x_1,2 = ± 24/2 = ± 12  

und die Gleichung  f(x) = a · x² + 8  (Scheitelform) 

f(12) = 0  →  144a + 8 = 0  →  a = - 1/18

→  f(x) =  -1/18 · x² + 8

Die eingebaute Tür hat dann Eckpunkte (u|f(u), (-u|f(u) auf der Parabel und (u|0), (-u|0) auf der x-Achse.

Ihre Fläche ist A(u) = 2u • f(u) = 2u · ( -1/18 · u² + 8) = -1/9 · u³ + 16u

Die maximale Fläche erhält man für A'(u) = -1/3 · u² + 16 = 0  und  A''(u) = -2/3 u < 0

  -1/3 · u² + 16 = 0  ⇔ u_1,2 = ± √(48) = ± √(16·3) =  ± 4 · √3   

A" ( 4 · √3) < 0 →  Maximum für  u = 4/3 · √3  ≈  6,93 

f(6,93) = 16/3 ≈ 5,33 

Die Tür mit maximaler Fläche ist also 13,86 m breit und 5,33 m hoch

Gruß Wolfgang

 

Answer 2

Du hast die Parabelgleichung f(x), unter diese musst du eine maximal große rechteckige Fläche bringen.

Diese Fläche hat die Höhe (in y- Richtung) f(x) und die Breite 2x, d.h. A(x)=2x*f(x). Diese Fläche musst du jetzt maximieren, was über Kurvendiskussion möglich ist (Ableitung bilden!).