Bestimme die Hesse Matrix von f(x,y)=176x^{0,26}y^{0,64}. Welchen Wert hat die detA?

Question

Aufgabe:

Bestimmen Sie die Hesse Matrix \( \boldsymbol{A} \) der Funktion

\( f\left(x_{1}, x_{2}\right)=176 x_{1}^{0.26} x_{2}^{0.64} \)

an der stelle \( \left(\begin{array}{l}1.7 \\ 9.5\end{array}\right) \).

Welchen Wert hat \( \operatorname{det} \boldsymbol{A} \)?

Answer 1

Hi,

ich nenne es mal f(x,y)=176x^{0,26}y^{0,64}

f_xx=-33,8624x^{-1,74}y^{0,64}

f_yy=-40,5504x^{0,26}y^{-1,36}

f_xy=f_yx=29,2864x^{-0,74}y^{-0,36}

 

Nun die Hesse-Matrix aufstellen.

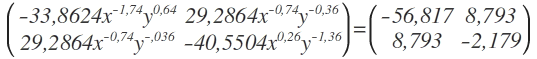
Ersteres ist die Hesse-Matrix und bei letzterem sind die Werte eingesetzt.

det A = -56,817*(-2,179)-(8,793)^2 = 46,487

 

In der Hoffnung mich nicht verrechnet zu haben und für Verständnis gesorgt zu haben,

 

Grüße

Comments

ein lösungsweg zu den ableitungen wäre super!!

danke

---

Hi,

ich mach das mal für

f_x und f_xx

Für f_x wird y als konstant betrachtet. Es ergibt sich:

f(x,y) = 176*x^{0,26}*y^{0,64}

f_x = 176*0,26*x^{0,26-1}*y^{0,64} = 45,76*x^{-0,74}*y^{0,64}

f_xx = 45,76*(-0,74)*x^{-0,74-1}*y^{0,64} = -33,8624*x^{-1,74}*y^{0,64}

 

Alles klar? ;)

Wichtig: Die nicht abzuleitenden Variablen sind als konstant zu betrachten, der Rest ist dann "ganz normal" ;).