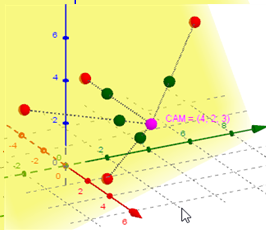
Von Kamera Z legen wir eine Gerade auf die Urbildpunkte. Gerade mit der Ebene schneiden führt auf eine Matrix in homogenen Koordinaten
(Bauanleitung https://www.geogebra.org/m/xwj3hnda)
\(\small Z_{CAM} \, := \, \left(\begin{array}{rrrr}-4&4&4&-4\\4&-10&2&-2\\6&3&-9&-3\\2&1&1&-13\\\end{array}\right)\)
Die Beispielpunkte
\(\small Fig \, := \, \left\{ \left(3, 2, 2 \right), \left(3, 1, 3 \right), \left(0, 5, 3 \right), \left(0, 2, 3 \right) \right\} \)
laden dann auf
\(\small Fig_H \, := \, \left\{ \left(\begin{array}{r}0\\-6\\3\\-3\\\end{array}\right), \left(\begin{array}{r}0\\6\\-9\\-3\\\end{array}\right), \left(\begin{array}{r}28\\-46\\-15\\-5\\\end{array}\right), \left(\begin{array}{r}16\\-16\\-24\\-8\\\end{array}\right) \right\} \)
normiert auf R³
\(\small FigZ \, := \, \left\{ \left(0, 2, -1 \right), \left(0, -2, 3 \right), \left(\frac{-28}{5}, \frac{46}{5}, 3 \right), \left(-2, 2, 3 \right) \right\} \)
Bild dazu