Fourierreihe einer Dreieckschwingung

Question

nachdem ich die Fourierreihe einer Rechteckschwingung und die einer Sägezahnschwingung berechnet habe, soll ich nun die Fourierreihe zu einer Dreieckschwingung berechnen.

x(t) = 1-|t| für -π<= t < π. Das Signal wird 2pi- periodisch fortgesetzt.

Anhand meiner Skizze erkenne ich, dass das Signal Symmetrisch zur y-Achse und somit ungerade ist.

Damit fallen die Quozienten b_n  weg.

Für a₀ habe ich

a₀ = $$ \frac { 1 }{ 2\pi  } \int _{ -\pi  }^{ \pi  }{ 1-|t|\quad dt\quad =\quad \frac { 2 }{ 2\pi  }  } \int _{ 0 }^{ \pi  }{ 1-t\quad dt\quad =\frac { 1 }{ 2\pi  }  } \cdot (x-\frac { { x }^{ 2 } }{ 2 } ){ | }_{ 0 }^{ \pi  }=\quad \frac { 1 }{ 2\pi  } \cdot (\pi -\frac { { \pi  }^{ 2 } }{ 2 } )=\frac { \pi  }{ 2\pi  } -\frac { { \pi  }^{ 2 } }{ 4\pi  } =\frac { 1 }{ 2 } -\frac { \pi  }{ 4 } $$

Irgendwie habe ich ein mulmiges Gefühl dabei, könnte mir jemand sagen ob ich das richtig gemacht habe?

Könnte mir noch jemand Tipps für a_n  geben?

Comments

Ja, das hast du richtig gemacht.

Heißen die \( b_n \) nicht Koeffizienten?

---

Hi, ich bin der Ersteller des Threads, musste mich registrieren um auf dein Kommentar zu antworten^^

Wow, freut  mich das ich das richtig gemacht habe! Dann mache ich mich gleich mal an a_n (werde ich dann auch noch hier reinschreiben, wäre nett wenn Sie, oder jemand anderes da auch noch drüber schauen könnten).

Ja das sollte Koeffizient heißen :)

---

Du müsstest oben noch irgendwo klicken können, dass die Frage von dir ist. (Dann steht dein Username da.)

---

Habe ich gemacht :)

Nochmal zu a_{n =}

$$\frac { 2 }{ 2\pi  } \int _{ -\pi  }^{ \pi  }{ 1-|t|cos(nt)\quad dt\quad =\quad \frac { 2 }{ \pi  } \int _{ 0 }^{ \pi  }{ (1-t)cos(nt)dt\quad \overset { * }{ = }  }  } \frac { 2 }{ \pi  } -\quad \frac { \pi n\quad sin(\pi n)\quad +cos(\pi n)-{ \pi n }^{ 2 }-1 }{ { n }^{ 2 } } $$

Beim zweiten "=" habe ich das ganze Ding durch folgenden Integralrechner laufen lassen:http://www.integralrechner.de/ , denke das sollte stimmen.

Da ich weiß, dass sin (πn) immer null wird,  bleibt der cos Teil, der  je nachdem ob n gerade oder ungerade zu 1 oder -1 wird. Somit habe ich zwei Fälle zu betrachten:

$$ Fall\quad 1:\quad n\quad =\quad gerade\quad ->\quad \frac { 2 }{ \pi  } \cdot (-\frac { 0+1-\pi { n }^{ 2 }-1 }{ { n }^{ 2 } } )\quad =\frac { 2 }{ \pi  } \quad \cdot \pi \quad =2\\ Fall\quad 2:\quad n=\quad ungerade\quad ->\frac { 2 }{ \pi  } \cdot (-\frac { 0-1-\pi { n }^{ 2 }-1 }{ { n }^{ 2 } } )\quad =\frac { 2 }{ \pi  } \cdot \quad \frac { \pi { n }^{ 2 }+2 }{ { n }^{ 2 } } \quad =\frac { 2\pi { n }^{ 2 }+4 }{ { \pi n }^{ 2 } }  $$

Hoffe das stimmt so.

Wäre dankbar wenn du oder jemand nochmal draufschauen könntet^^

---

Das Integral kommt mir komisch vor. Kannst du es nochmal selbst ausrechnen? Der von dir angegebene Integralrechner schlägt einen Lösungsweg vor, an dem du dich orientieren kannst.

Answer 1

habe mal den FFT-Faktor

(2Pi*n²+4)/(Pi*n²)=2+4/(PI*n²) mit

http://www.lamprechts.de/gerd/Liniendiagramm_Scientific_plotter.htm

Beispiel 116 getestet (Dein n ist dort aB[0]

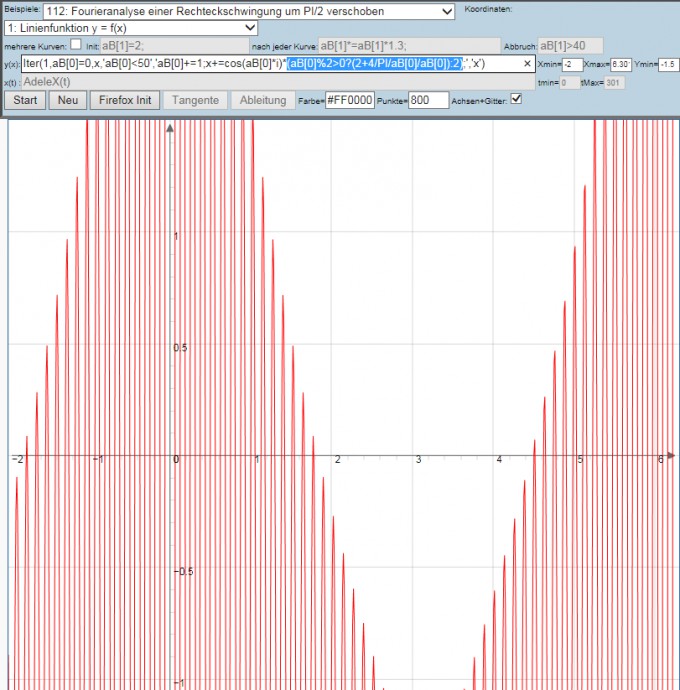
Bild sah nicht gut aus -> also selbst nachgerechnet

#

∫ (1-abs(t))*cos(n*t)dt,t=-Pi...Pi

= -(2 ((pi-1) n sin(pi n)+cos(pi n)-1))/n^2

=(2-2cos(pi n)-2(pi-1)*n*sin(pi n))/n^2

noch durch Pi, also was vor dem Integral war -> ergibt den gesuchten Faktor:

(2-2*cos(aB[0]*PI)-2*(PI-1)*aB[0]*sin(aB[0]*PI))/pow(aB[0],2)/PI

beide Kurven im Vergleich: rote 1-abs(x) grün die aufsummierte cos-Reihe:

aB[1]<1?1-abs(x):Iter(1,aB[0]=0,x,'aB[0]<50','aB[0]+=1;x+=cos(aB[0]*i)*(2-2*cos(aB[0]*PI)-2*(PI-1)*aB[0]*sin(aB[0]*PI))/pow(aB[0],2)/PI;','x')+1-PI/2

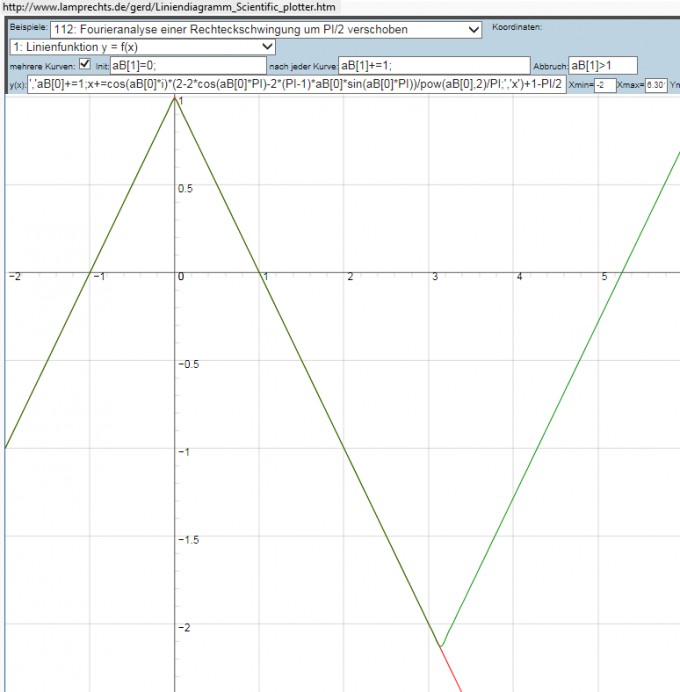
Bild 2 OK -> zeigt Übereinstimmung:

Optimierung, da man für ganze n keine komplizierte sin/cos braucht: cos(Pi*n)=(-1)^n

(2-2*cos(n*PI)-2*(PI-1)*n*sin(n*PI))-> ist die 0,4,0,4 Folge (2-2*(-1)^n)

also einfach

=(2-2*(-1)^n)/(PI*n^2) -> kompatibel (2-2*pow(-1,aB[0]))/pow(aB[0],2)/PI

Test:

aB[1]<1?1-abs(x):Iter(1,aB[0]=0,x,'aB[0]<50','aB[0]+=1;x+=cos(aB[0]*i)*(2-2*pow(-1,aB[0]))/pow(aB[0],2)/PI;','x')+1-PI/2

Bild 3: nun alles OK

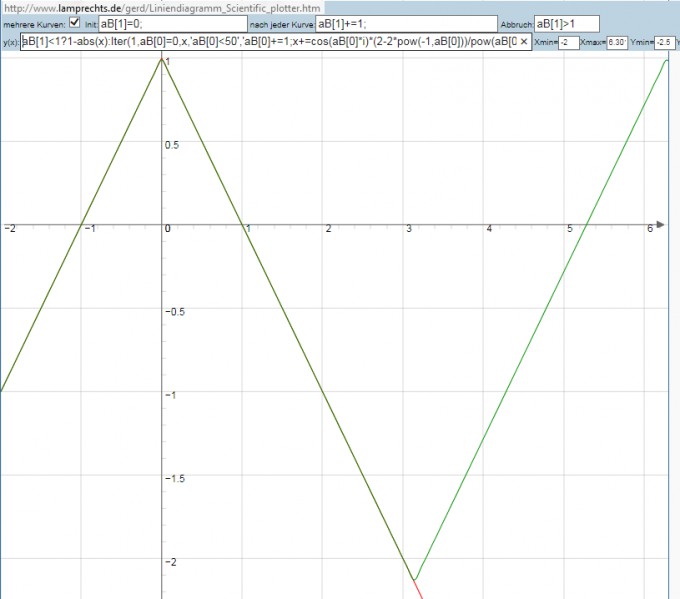
Interessant ist noch a₀, also die y-Verschiebung:

Ihr hattet 1/2-PI/4 statt meiner +1-PI/2

∫ (1-abs(t))/Pi dt,t=-Pi...Pi = 2-Pi überprüft mit 

https://www.wolframalpha.com/input/?i=integrate+(1-abs(t))%2FPi+dt,t%3D-Pi...Pi

dann die Hälfte ergibt  1-PI/2

siehe

https://de.wikipedia.org/wiki/Fourierreihe

Comments

Vielen Dank HyperG. Bin mit dem Beispiel so weit gekommen das ich fast vergessen hätte mich hier zu bedanken :)Hat mir sehr geholfen!