Aufgabe:
ich habe folgende Aufgabe die ich schon gelöst habe und mit den Ergebnissen der Musterlösung kontorlliert habe. Mein Problem ist nur, dass ich nicht wirklich weiß, wie ich auf die \( \frac{4}{T} \) komme. Ich habe in einem anderen Forum gefragt aber irgendwie keine konkrete Antwort bekommen. Ich habe mal eine Skizze davon erstellt, damit man mein Verständnisproblem besser nachvollziehen kann.
Bestimmen Sie die Fourier-Reihen zu den 2π -periodischen Fortsetzungen von
\( f(t)=|t|, t∈(-π,π], \)
\( g(t) =\left\{\begin{array}{ll} 1 \quad für \quad -π<t≤0 \\ -1\quad für\quad 0≤t≤π \end{array}\right. \)
Text erkannt:
Bestimmen Sie die Fourier-Reihen zu den \( 2 \pi \)-periodischen Fortsetzungen von
\( f(t)=|t|, t \in(-\pi, \pi], \quad g(t)=\left\{\begin{aligned} 1 & \text { für }-\pi<t<0 \\ -1 & \text { für } \quad 0 \leq t \leq \pi \end{aligned}\right. \)
Problem/Ansatz:
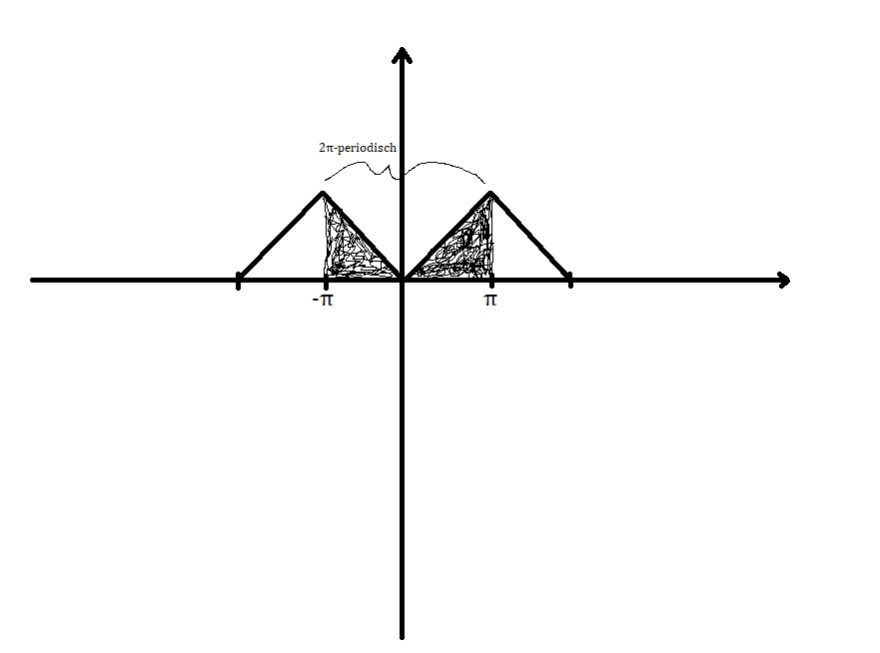
Gegeben ist eine Dreiecksfunktion die sich 2π periodisch fortsetzt. Also immer von -π bis π (siehe Skizze). Meine Frage lautet, wie ich jetzt erkenne, wann ich \( \frac{4}{T} \) schreibe und wann \( \frac{2}{T} \)? Müsste hier nicht \( \frac{2}{T} \) stehen? \( \frac{1}{T} \) spiegelt doch die Frequenz wieder und daher ist sie Abhängig von der Periode. Es handelt sich hierbei um eine gerade Funktion,daher fällt ja dann auch \( b_{n} \) weg.
Kann mir jemand erklären, wie ich immer zu Beginn rausfinden kann, ob da 2/T oder 4/T stehen muss? Ich weiß das ist eine dumme Frage, aber mittlerweile bin ich so verwirrt. Das liegt einfach daran, dass mir jeder etwas anderes erzählt hat, auch Leute die dieses Thema selber nicht verstanden haben.
\( a_{0} = \frac{4}{T} \int\limits_{0}^{π} t \quad dt \)
\( a_{n} = \frac{4}{T} \int\limits_{0}^{π} t \cdot cos(n\cdot t) \quad dt \)
Text erkannt:
NA