Tangentengleichung bestimmen. Gleichung des Kreises lautet (x-5.7)^2 + y^2 = 3.5^2

Question

ich muss an einem bestimmen Punkt an Kreisrand ( Punkt (2.7 / 1.789 ) ) eine Tangentengleichung bestimmen. DIe Gleichung des Kreises lautet (x-5.7)^2 + y^2 = 3.5^2 .

!!!

Comments

Hast du den Punkt richtig ausgerechnet? Soll der Punkt auf dem Kreis liegen?

Man kann von beliebigen Punkten ausserhalb des Kreises jeweils zwei Tangenten an den Kreis legen.

Die Formulierung hinkt etwas.

Wenn P auf dem Rand liegt,  kannst du das übrigens auch mit Vektorgeometrie machen.

Der Vektor MP steht senkrecht auf dem Richungsvektor der Tangente.

Answer 1

Kreisgleichung:

(x-5.7)^2+y^2-12.25=0

(x-5.7)^2+f(x)^2-12.25=0 implizit differenzieren:

2*(x-5.7)+2*f(x)*f'(x)=0

--> f'(x)=-(x-5.7)/f(x)=-(x-5.7)/y

x und y einsetzen:

f'(2.7)=m=3/1.789=1.6769

--> t(x)=1.6769*(x-2.7)+1.789

oppps die Werte liegen nicht auf dem Kreis -__-

~plot~ sqrt(-(x-5.7)^2+12.25);1.6769*(x-2.7)+1.789 ~plot~

Comments

für die richtigen Werte:

x=2.7 und y=1.8028:

m=1.664078

t(x)=1.664078*(x-2.7)+1.8028

---

Auch 1,8028 ist nicht der richtige Wert. Dieser ist √3,25.

---

Ich weiß schon, aber das Zeichenprogramm erkennt kein Wurzelzeichen und da hab ich Werte runden müssen  und hab die dann in der Formel so hin geschrieben damit es konsistent bleibt.

Answer 2

Der angegebene Punkt liegt nicht auf dem Kreis sondern im Inneren des Kreises. Man kann also nicht eimal eine Tangente an den Kreis durch diesen Punkt legen.

Answer 3

Text erkannt:

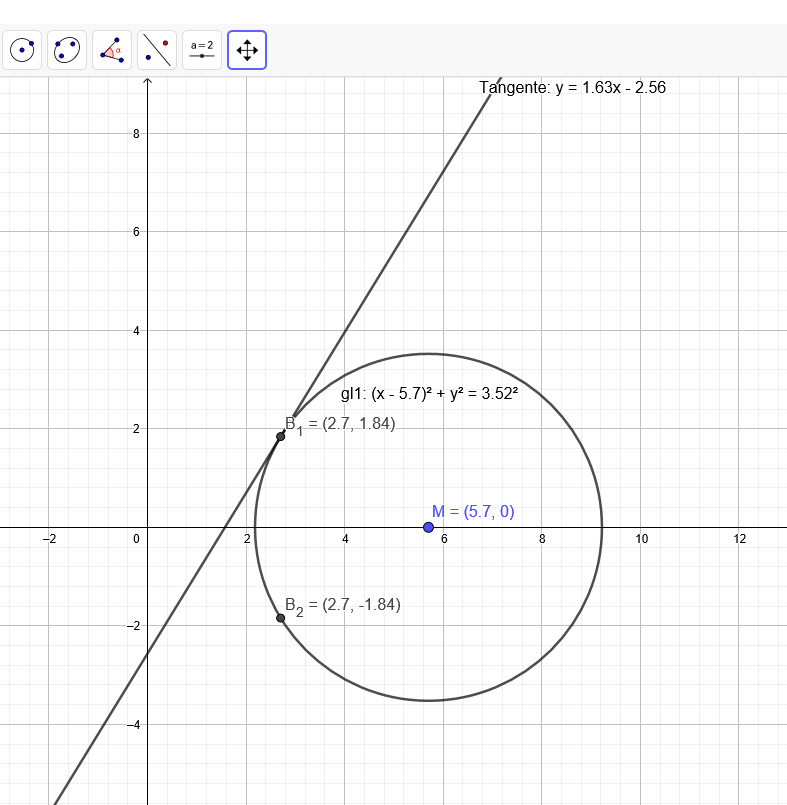
\( (x-5,7)^{2}+y^{2}=3,52^{2} \)
\( B_{1}(2,7 \mid 1,8413) \) und \( B_{2}(2,7 \mid-1,8413) \)
Mittelpunkt des Kreises:
\( M(5,7 \mid 0) \)
Steigung der Geraden durch \( M(5,7 \mid 0) \) und \( B_{1}(2,7 \mid 1,8413) \)
\( m=\frac{1,8413-0}{2,7-5,7} \rightarrow \rightarrow \) Steigung der Tangenten: \( m_{T}=\frac{-2,7+5,7}{1,8413-0} \approx 1,63 \)
Tangentengleichungen
\( \frac{y-1,8413}{x-2,7}=1,63 \)
1.) \( y=1,63 x-2,56 \)
Da der Mittelpunkt des Kreises auf der \( x \) -Achse liegt, gilt:
2. \( ) y=-1,63 x+2,56 \)

Text erkannt:

6