also ich habe das Integral 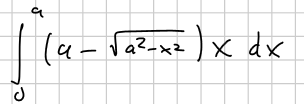
Substituton: u= a^2-x^2 -> dx= - du/2x
∫(a-√(u)*x *(-du/2x) = -1/2 *∫a-√(u)du = -1/2 [ a*u-2*(u)^{3/2} ] = resub => -1/2 [a*(a^2-x^2)-2*(a^2-x^2)^{3/2}]
jetzt die Grenzen einsetzen -> -1/2*[0-0-a^3+2a^3] 0= -a^3/2
Die Lösung sagt aber, dass da -a^3/6 rauskommt und ich weiß einfach nicht wie man drauf kommt