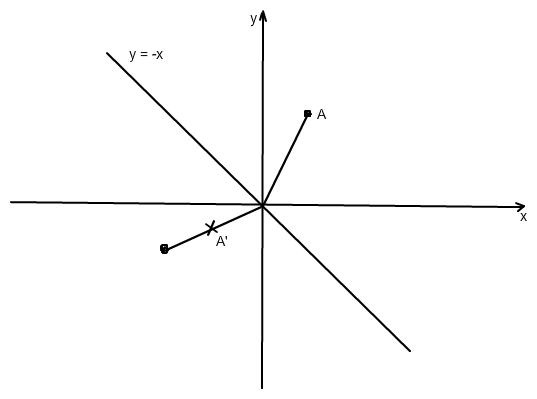
\(\begin{pmatrix} x \\ y \end{pmatrix}\) ↦ \(\begin{pmatrix} -y \\ -x \end{pmatrix}\) ↦ \(\begin{pmatrix} -1/2·y \\ -1/2· x \end{pmatrix}\)
\(\begin{pmatrix} a&b\\ c&d\end{pmatrix}\) • \(\begin{pmatrix} x \\ y \end{pmatrix}\) = \(\begin{pmatrix} ax + by \\ cx + dy \end{pmatrix}\) = \(\begin{pmatrix} -1/2·y \\ -1/2·x \end{pmatrix}\)
die letzte Gleichung muss für alle (x,y) ∈ ℝ2 gelten:
(0,1) → b = -1/2 und d = 0
(1,0) → a = 0 und c = -1/2
→ gesuchte Matrix A = \(\begin{pmatrix} 0&-1/2\\ -1/2&0\end{pmatrix}\)
→ f(x) = \(\begin{pmatrix} 0&-1/2\\ -1/2&0\end{pmatrix}\) • \(\begin{pmatrix} x \\ y \end{pmatrix}\)
Gruß Wolfgang
