Beispiel maximales Quadrat in einer Parabel ermitteln zwei Wege

Question

ich glaube gestern wurde hier nachgefragt. Wie sieht ein maximales Quadrat in einer Parabel aus.

Nun es gibt mehrere Ansätze, die ich mir überlegt habe. Siehe dazu das Bild

Zum roten Quadrat:

Ich denke es ließe sich so ausrechnen:

x = -x^2 + 9

-x^2 + x - 9 PQ Formel:

--> 2,4

Das Quadrat hätte damit eine Länge a von 2,4 LE

Zum grünen Quadrat:

Mein Ansatz wäre hier ein Rechteck zu wählen, welches maximal wird. Beispielsweise könnten wir das grüne Quadrat teilen und eine Rechtecksfläche ermitteln. Ist das ein richtiger Ansatz? 

Kann ich aus dem Maximalen Rechteck der rechten Seite ein Maximales Quadrat bilden (also das grüne)?

Answer 1

" Wie würde denn rechnerisch das maximale Quadrat (grün) aussehen? ".

Das habe ich doch gestern bei der erwähnten Frage schon vorgerechnet. Analog zu dort kannst du ansetzen: 

2x = 9 - x^2  

Dein Ansatz für das rote Quadrat 

x = -x² + 9

x² + x - 9 = 0  | PQ-Formel

--> 2,54

stimmte übrigens. 

Es kommt halt immer auf die exakte Fragestellung an, wenn man entscheiden muss, wie man das zeichnet und rechnet.

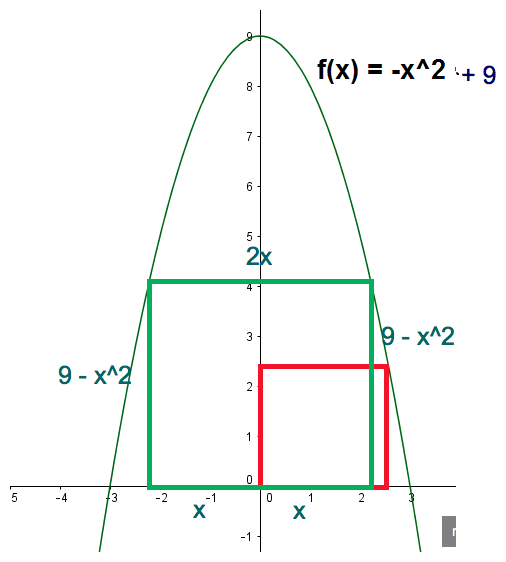
Hier würde man vom grössten Quadrat, das zwischen Parabel und x-Achse eingeschlossen ist, sprechen. 

Man könnte auch sagen "dem Bogen zwischen der Parabel und der x-Achse ist ein Quadrat einzubeschreiben". Also ist das grüne Quadrat ein sog. einbeschriebenes Quadrat.

und dann noch das rote Quadrat

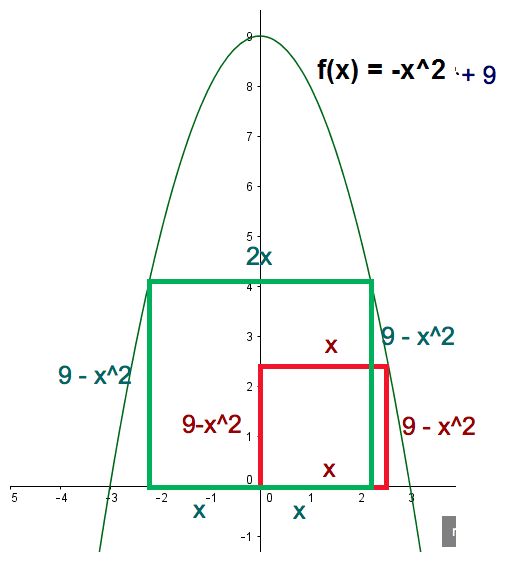
Das rote Quadrat liegt im ersten Quadranten und ist zwischen y-Achse, x-Achse und der Parabel eingeschlossen. 

Answer 2

Schon die Antwort fürs rote Quadrat ist falsch. Fürs grüne Quadrat mit der Seitenlänge x findet man den Ansatz  x/2=f(x/2) oder x/2 = -(x/2)²+9. Die für die p-q-Formel taugliche Gleichung lautet dann x²+2x-36 = 0.

Comments

Stimmt x/2 jap und dann die PQ, logisch.

Warum sollte die Berechnung für das rote Quadrat falsch sein?

---

Der Ansatz für das rote Quadrat ist richtig. Aber dann kommt  2,54 heraus und nicht 2,4.

Aber mein Ansatz fürdas grüne Quadrat ist falsch. Er muss heißen: 2x = f(x) oder 2x = -x²+9. Die Quadratseite ist dann 2x.

---

Aber mein Ansatz fürdas grüne Quadrat ist falsch. Er muss heißen: 2x = f(x) oder 2x = -x²+9. Die Quadratseite ist dann 2x. 

--> Genau, so macht es mehr Sinn. :-)

Answer 3

Nein das geht nicht. Ein maximales Rechteck hat nicht unbedingt das seitenverhältnis 2:1, welches aber nötig ist um ein Quadrat daraus bilden zu können durch verdopplung.

Comments

Das habe ich fast befürchtet. Wie würde denn rechnerisch das maximale Quadrat (grün) aussehen?