Bestimme Lösungsmenge Ungleichungen mit Betrag | 3x + 2 |< 5x - 1

Question

Könnte mir jemand bitte bei folgenden Aufgabe helfen ich habe selber ein Ansatz.

Bestimmen Sie die lösungsmengen  der folgenden ungleichungenin ℕ, ℤ, ℝ.

a. | 3x + 2| < 5x -1 

Fall 1: x < -2/3

-3 - 2 < 5x -1 

-1 < 3x

- 1/3 < x

] - ∞ ; -1/3 [ 

Fall 2:  - 2/3 >= x > - 1/3 (macht das Sinn?)

b. | |2x + 3| + |3x| | <= 4x

Danke für  jede Hilfe. :)

Comments

~plot~ abs(abs(2x + 3) + abs(3x) );[[20]] ; 4x ~plot~

Zeigt dir, dass L = { ...} . [Leere Menge] 

Weitere Ungleichungen mit Betrag findest du bei den "ähnlichen Fragen". 

Answer 1

 

a)

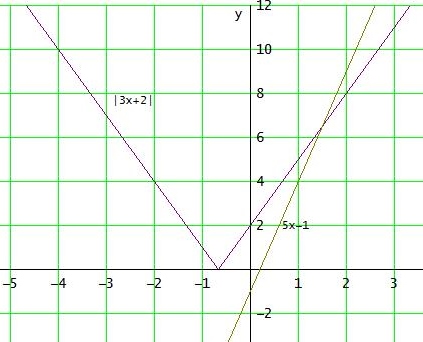
| 3x + 2| < 5x -1 

Fall 1: x < -2/3   ( 3x+2 < 0 )

Der Betrag kann entfallen, wenn man ein Minuszeichen vor den Term setzt  

[ z.B. | (-3) | = -(-3) = 3 ]

-3x - 2 < 5x -1     | +1   | : 8

  -1 <  8x   ⇔ x > -1/8   →   L₁ = {  }

> Fall 2:  - 2/3 >= x > - 1/3 (macht das Sinn?)

Nein:

Fall 2:  3x+2 ≥ 0, also  x ≥ -2/3      

Der Betrag fällt einfach weg   [  | 3| = 3 ]

3x + 2 < 5x - 1

   3x + 2 < 5x -1  ⇔  3 < 2x  ⇔  3/2 < x  →  L₂ = ] 3/2 ; ∞ [

  L = L₁ ∪ L₂ = ] 3/2 ; ∞ [ 

----------

b)  

Der Term im äußeren Betrag ist als Summe zweier Beträge ≥ 0. Die äußeren Betragstriche kann man also weglassen:

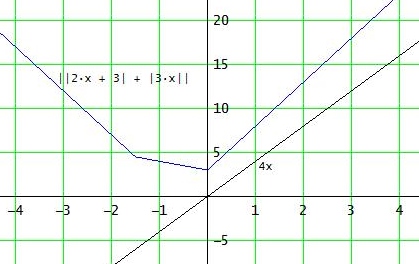
|2x + 3| + |3x|  ≤ 4x

Die Nullstellen in den Beträgen sind  x= -3/2 und x=0

Vorzeichen der Terme in den  Beträgen:

                                                       x < -3/2                -3/2 ≤ x ≤ 0                  x >0

                                  2x + 3                -                              +                             +

                                     3x                   -                               -                              +

linke Seite:                                   -2x-3 - 3x                 2x+3 - 3x                 2x+3 + 3x

                                                        -5x-3                          -x+3                         5x+3

Fall 1:   x < - 3/2   

-5x - 3 ≤ 4x  ⇔  - 3 ≤ 9x    →  -1/3 ≤ x   →  L₁ = { }  

Fall 2:   -3/2 ≤ x ≤ 0  

-x + 3 ≤ 4x  ⇔ 3 ≤ 5x  ⇔  x ≥ 3/5   →  L₂ = { }

Fall 3:  x > 0  

5x+3 ≤ 4x   ⇔  x ≤ -3   →   L₃ = { }

L = L₁ ∪ L₂ ∪ L₃   = { }

Gruß Wolfgang 

Comments

VIELEN DANK FÜR DEINE HILFE,

Fragen habe ich aber noch:

Erstmal zu a:

1. Warum ist die lösungsmengen bei dem ersten Fall leer?

2. Muss man sich einer Gleichung die betragstriche enthält immer ein mal > 0 oder <= 0 nähren

3. Wann weißt ich wenn ich die betragstriche entfernen möchte ob sich das Vorzeichen ändert?

4. Ist es ein halboffenes Intervall weil x kleiner als 3/2 ist und man nicht genau was was genau x ist?

!!

---

1)  x kann nicht gleichzeitig ≥ -1/3 und ≤ -3/2 sein  

2)  | A | = A , wenn A ≥ 0 ist und | A | = - A , wenn A < 0 ist

3)  Wenn du - wie oben - nur einzelne Beträge und die Nullstellen der Terme in diesen Beträge hast, kann sich das Vorzeichen dieser Terme nur innerhalb der durch die Nullstellen festgelegten Intervalle ändern (wenn der jeweilige Term stetig ist).

Um das jeweilige Vorzeichen zu bestimmen kannst du dann einfach jeweils einen Wert aus den einzelnen Intervallen einsetzen.

4)  Ob die Intervalle offen oder abgeschlossen sind, hängt davon ab, ob in der Ungleichung  > bzw. < ober ≥ bzw. ≤ steht. 

----

Beispiel:   | x - 4 |  ≤  5   

x - 4 = 0  →  Nullstelle x = 4

In ] -∞ ; 4 ]  kann man in den Term x-4   z.B.   x=0, in ] 4 ; ∞ [  x=5 einsetzen 

→ Vorzeichen in  ] -∞ ; 4 ]  negativ, in ] 4 ; ∞ [  positiv

→ | x - 4 | = - (x-4) = -x + 4  in  ] -∞ ; 4 ]

     | x - 4 | =  x -4  in  ] 4 ; ∞ [   

Dabei ist es gleichgültig, zu welchem Intervall die Nullstelle x = 4 dazunimmst.

---

Danke, aber ich verstehe immer noch nicht so ganz wie man das Vorzeichen bestimmt wenn man die betragstriche löst 

Warum ist |3x +2| hier negativ : x < - 2/3

Könntest du mir vielleicht als Übung  auch eine Ungleichung geben die ich lösen muss?

---

Nach langem Überlegen habe ich festgestellt, dass wenn man die Nullstellen hat z.b. x= 5 die Gleichung umschlossen von betragstriche ist erst positiv wenn x>= 5 ist und wenn dies nicht der Fall ist dann negativ. Stimmt es??

---

Warum ist |3x +2| hier negativ : x < - 2/3 ?

3 x + 2 = 0  ⇔  x = - 2/3  

durch Einsetzen von z. B.  x=-10 und x=0 siehst du:

Für jeden x-Wert mit x < -2/3  ist   3x + 2 negativ, für x-Werte mit x > -2/3 postiv

deshalb:

für x < -2/3      |3x+2| = - (3x+2) = -3x - 2

für x > -2/3      |3x+2| = 3x+2 

Übung:

| 3x - 6 | >  x          L = ] − ∞ ; 3/2 [  ∪ ] 3 ; ∞ [

---

DANKE!!

| 3x - 6 | >  x  

Nullstelle: x=2 

1. Fall x <2

-3x +6 > x

6 <  4x 

3/ 2 <x

L  [ 3/2; 2 [

2. Fall   x>= 2

3x - 6 >= 2

3x >= 8

x >= 8/3

Was mache ich falsch??

---

Bei den einzelnen Fällen ändert sich auf der rechten Seite der Ungleichung erst einmal nichts!

1. Fall x <2

-3x +6 > x  ← !

→    6  >   4x  →  x < 3/2  →  L₁ = ] −∞ ; 3/2 [

2. Fall   x>= 2

3x - 6 >= x  ← !

2x >= 6

x >= 3    →   L₂ = ] 3 ; ∞ [ 

---

Oh man wenn ich gerade so sehe was für "dumme" Fehler ich gerade gemacht habe. Hast du vielleicht noch eine letzte Übung?

---

| 4x + 8 | < -2x                 L = ] -4 ; -4/3 [

---

|4x + 8| < 2x 

Nullstelle: x=-2

1. Fall x < -2

-4x -8 < 2x

-8 < 6x

-4/3 < x

L1 = ] -2 ,-4/3 [

2. Fall x>= -2

4x + 8 < 2x

8 < -2x

-4 > x

L2 = ]-4 ; -2 [

L= ]-4 ; -4/3 [

So wie findest du das?

Eine Frage zu den Intervallen in welchem Beispiel ware der Intervall eindeutig geschlossen?

Danke

---

Das ist nicht meine Aufgabe :-)       | 4x + 8 | < - 2x 

1. Fall x < -2

-4x -8 < 2x

-8 < 6x

-4/3 < x   bis hierher richtig         

L1 = ] -2 ,-4/3 [  f           L₁ = {  } 

2. Fall x>= -2

4x + 8 < 2x

8 < -2x

-4 > x    bis hierher richtig         

L2 = ]-4 ; -2 [ f        L₂ = {  } 

L= ]-4 ; -4/3 [ f         L = {  }

Answer 2

$$ \text{zu a)}\quad \left| 3x + 2\right| < 5x -1  $$
Offenbar muss \(x>0\) gelten, um die Ungleichung zu erfüllen. Daher sind die Betragsstriche entbehrlich und die Ungleichung ist äquivalent zu
$$\dots \quad\Leftrightarrow\quad 3x + 2 < 5x -1 \quad\Leftrightarrow\quad 1.5 < x $$Die jeweiligen Lösungsmengen für die drei verschiedenen Grundmengen ergeben sich entsprechend.

Comments

$$ \text{zu b)}\quad \left| \left|2x + 3\right| + \left|3x\right| \right| \le 4x $$Offenbar wird die Ungleichung nur erfüllt, wenn \(0\le x\) gilt. Beschränken wir uns nun auf diesen einzig relevanten Fall, kann keines der drei Betragsargumente negativ werden, die Betragsklammern sind daher entbehrlich und wir lassen sie weg. So entsteht das äquivalente System
$$ \Leftrightarrow\quad 2x + 3 + 3x \le 4x \quad\land\quad 0\le x$$welches wegen
$$ \Leftrightarrow\quad x \le -3 \quad\land\quad 0\le x$$offensichtlich unabhängig von der gewählten Grundmenge jeweils nur leere Lösungsmengen besitzen muss.

Answer 3

$$|3x+2|<5x-1$$ Es muss folgendes gelten $$5x-1>0 \Rightarrow x>\frac{1}{5}$$ Wenn |y|<a dann -a<y<a. Also $$-(5x-1)<3x+2<5x-1$$ Wir lösen die 2 Ungleichungen getrennt. $$-5x+1<3x+2 \Rightarrow 8x>-2 \Rightarrow x>-\frac{1}{4}$$ $$3x+2<5x-1 \Rightarrow 2x>3\Rightarrow x>\frac{3}{2}$$ 
Also haben wir folgende Lösungsmenge: $$x\in \left(\frac{1}{5}, +\infty \right)\cup \left(-\frac{1}{4}, +\infty \right)\cup \left(\frac{3}{2}, +\infty \right)=\left(\frac{3}{2}, +\infty \right) $$

Comments

Mindestens die die letzte Zeile ist falsch.

Answer 4

Hi,

b)

||2x+3|+|3x||<=4x

Fallunterscheidung: x<0:

--> linker Term positiv, rechter Term negativ, keine Lösung

x>=0:

beide Seiten positiv, quadrieren ist also Äquivalenzumformung:

(|2x+3|+3|x|)^2<=16x^2

(2x+3)^2+9*x^2+6*|2x+3|*|x|<=16x^2

4x^2+12x+9+9*x^2+6*|2x+3|*|x|<=16x^2

13x^2+12x+6*(2x^2+3x)+9<=16x^2

25x^2+30x+9<=16x^2

keine Lösung (linke Seite ist immer größer)

Comments

Quadrieren im 2. Fall ist eigentlich nicht nötig.

||2x+3|+|3x||<=4x

Fall:   x<0:

--> linker Term positiv, rechter Term negativ, keine Lösung

Fall x>=0: Die Betragsstriche links bewirken gar nichts mehr

2x+3+ 3x <= 4x

5x + 3 ≤ 4x

x≤ - 3   steht in Widerspruch zu x≥0. ==> Keine weitere Lösung.