Geben Sie den maximalen Definitionsbereich als Teilmenge in R an. g(x) = √((ln(x))^3-ln(x^8)+3)

Question

Ich benötige etwas Hilfe den maximalen Definitionsbereich folgender Funktionen zu bestimmen.

1. f(x) = arcsin(ln(x))

2. g(x) = √((ln(x))³-ln(x⁸)+3)

Answer 1

1. f(x) = arcsin(ln(x))

Arcsin(u) hat den Definitionsbereich D =  [-1 , +1] 

D.h. nun 

-1 ≤ u ≤ 1 

also:

-1 ≤ ln(x) ≤ 1 

.

Nun mal die Eckpunkte des Definitionsbereichs von f :

ln(x) = -1

x= e^{-1} = 1/e

ln(x) = 1

x = e^{1} = e

D_(f) = [ 1/e, e ]

Gib das in den Taschenrechner ein, falls ihr das dezimal angeben sollt.

Kontrolle mit:

https://www.wolframalpha.com/input/?i=arcsin(ln(x))

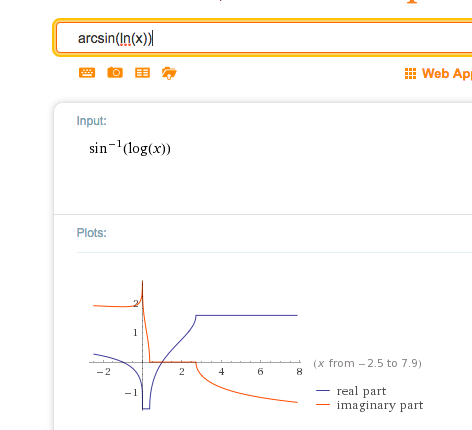
Es ist nur der Bereich relevant, in dem der Imaginärteil 0 ist. Also der Bereich, in dem der blaue (reelle) Graph steigt. Das ist der Graph der Funktion f. 

2. g(x) = √((ln(x))³-ln(x⁸)+3) 

Wähle 

u = ((ln(x))³-ln(x⁸)+3)

Du weisst (wegen der Wurzel), dass u≥ 0 sein muss. 

D.h. du kümmerst dich jetzt um

((ln(x))³-ln(x⁸)+3) ≥ 0 , um den Definitionsbereich von g zu bestimmen. 

Wegen ln(x) muss gelten, dass x> 0 ist.

((ln(x))³-ln(x⁸)+3) ≥ 0

((ln(x))³- 8 ln(x)+3) ≥ 0      | Substitieren ln(x) = v

v^3 - 8 v + 3 ≥ 0

Nun kannst du erst mal alles nachrechnen, gegebenenfalls korrigieren und dann dieses Polynom

h(v) = v^3 - 8 v + 3

  diskutieren. Du brauchst (nur) die Nullstellen. Eine von ihnen ist übrigens "minus drei".

Damit dann z.B. Polynomdivision machen. usw.