Sinus, Cosinus und Tangens: Wie berechnet man die Höhe '?'? (Gegenkathete)

Question

Wie soll man '?' berchenen? Mit welcher Formel?

Answer 1

Das ist ein mehrstufiger Berechnungsvorgang.

Schau mal ob du es anhand meiner Berechnung nachvollziehen kannst. Ich habe die Seiten aber ziemlich dumm beschriftet.

Comments

Danke für den Ansatz aber aber man kann b nicht mit sinus berechnen, da das nur für ein rechtwinkliges Dreieck  gilt oder? :O

---

Stichwort: Sinussatz

Der gilt für alle Dreiecke und nicht nur für rechtwinklige.

Answer 2

Alternative: Falls du den Sinussatz noch nicht kennst. Höhe: x. kleiner Abschnitt unten y.

tan B = x/y

tan A = x/(y+200)

Jetzt gibt's einfach etwas mehr zu rechnen. Du hast aber 2 Gleichungen für 2 Unbekannte.
Beide mal Hauptnenner

y tan B = x

(y + 200) tan A = x

Da beide =x

y tan B = (y+200) tan A

y tan B = y tan A + 200 tan A

y tan B - y tan A = 200 tan A

y(tan B - tan A) = 200 tan A     |: (tan B - tan A)

y = 200 tan A / (tan B - tan A)

Da x = y tan B folgt

x = 200 tan A * tan B / ( tan B - tan A)

Wenn du das nun in den Taschenrechner eingibst sollte dasselbe rauskommen wie beim Sinussatz vgl. Rechnung von Mathecoach. Ansonsten: Bitte Rechenfehler suchen.

Comments

Auch ein sehr schöner Ansatz

TAN(a)·TAN(b)/(TAN(b) - TAN(a))

Wenn man hier den tan gemäß Definition als sin/cos schreibt erhält man

SIN(a)·SIN(b)/(COS(a)·SIN(b) - SIN(a)·COS(b))

Nach Anwendung eines Additionstheorems auf den Nenner folgt daraus

SIN(a)·SIN(b)/SIN(b - a)

Das ist auch das was man allgemein mit dem Sinussatz herausbekommt:

Höhenbestimmung von einer Standlinie aus

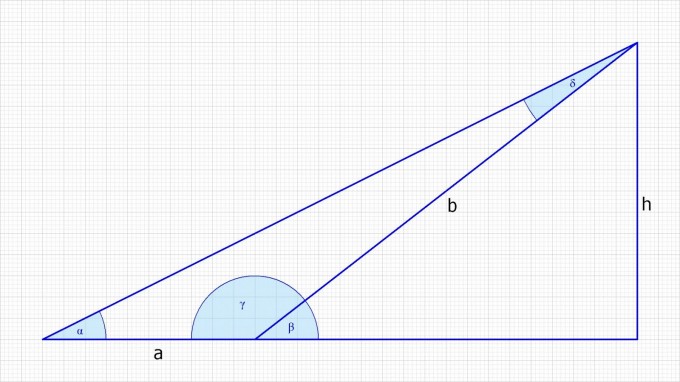
Gegeben sind a, α und β

γ = 180° - β

δ = 180°- α - γ = β - α

b = a / sin(δ) · sin(α) = a · sin(α) / sin(β - α)

h = b · sin(β)

h = a · sin(β) · sin(α) / sin(β - α)

---

Danke für die schöne Grafik. Ich werde ganz verrückt von dem ganzen rumgerechne.

Schaut auch mal hier: https://www.matheretter.de/wiki/skript-trigonometrie

Gibt auch paar Allgemeine Definitionen, kann sehr Hilfreich für Klausuren sein!